Plotmath fractals - coolbutuseless

Plotmath

plotmath is a little domain specific language within R used to define and display mathematical formula.

It looks just like R code, but is interpreted in a different context in order to make a math equation.

Writing x ^ 2 in R usually tries to evaluate what x-squared is, but in a plotmath expression, the symbols are interpreted as their relative arrangement in a mathematical formula.

Rendering the plotmath expression x ^ 2 instructs the plotmath rendering engine (usually via plot() or ggplot()) to write an x and then write 2 as a superscript (as indicated by the ^). This produces the following:

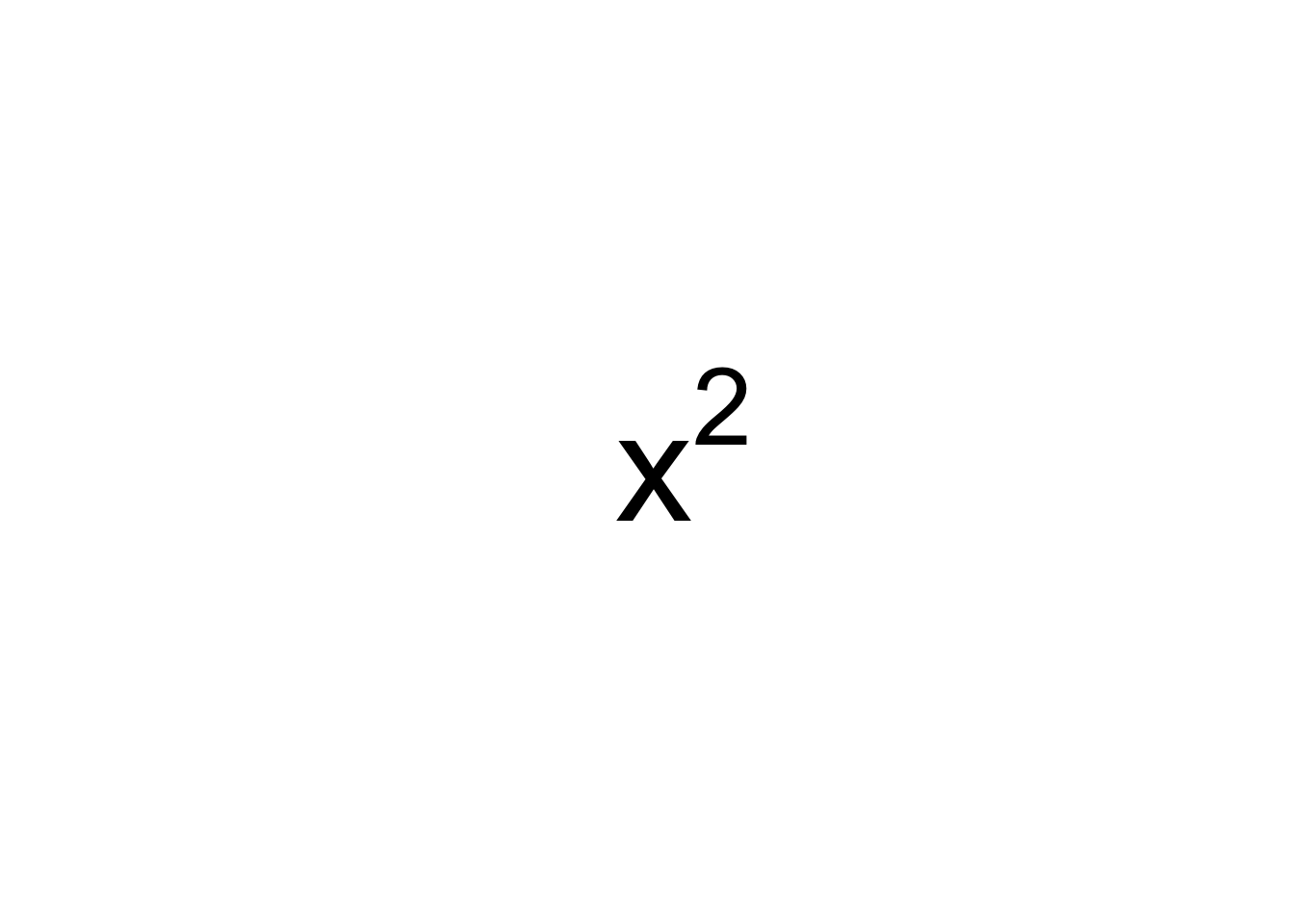
Creating Plotmath Expressions

The most flexible way to create a plotmath expression is to use bquote() (For a great introduction, see TRinkers R Blog )

bquote(infinity > italic("Any number you can think of")^2)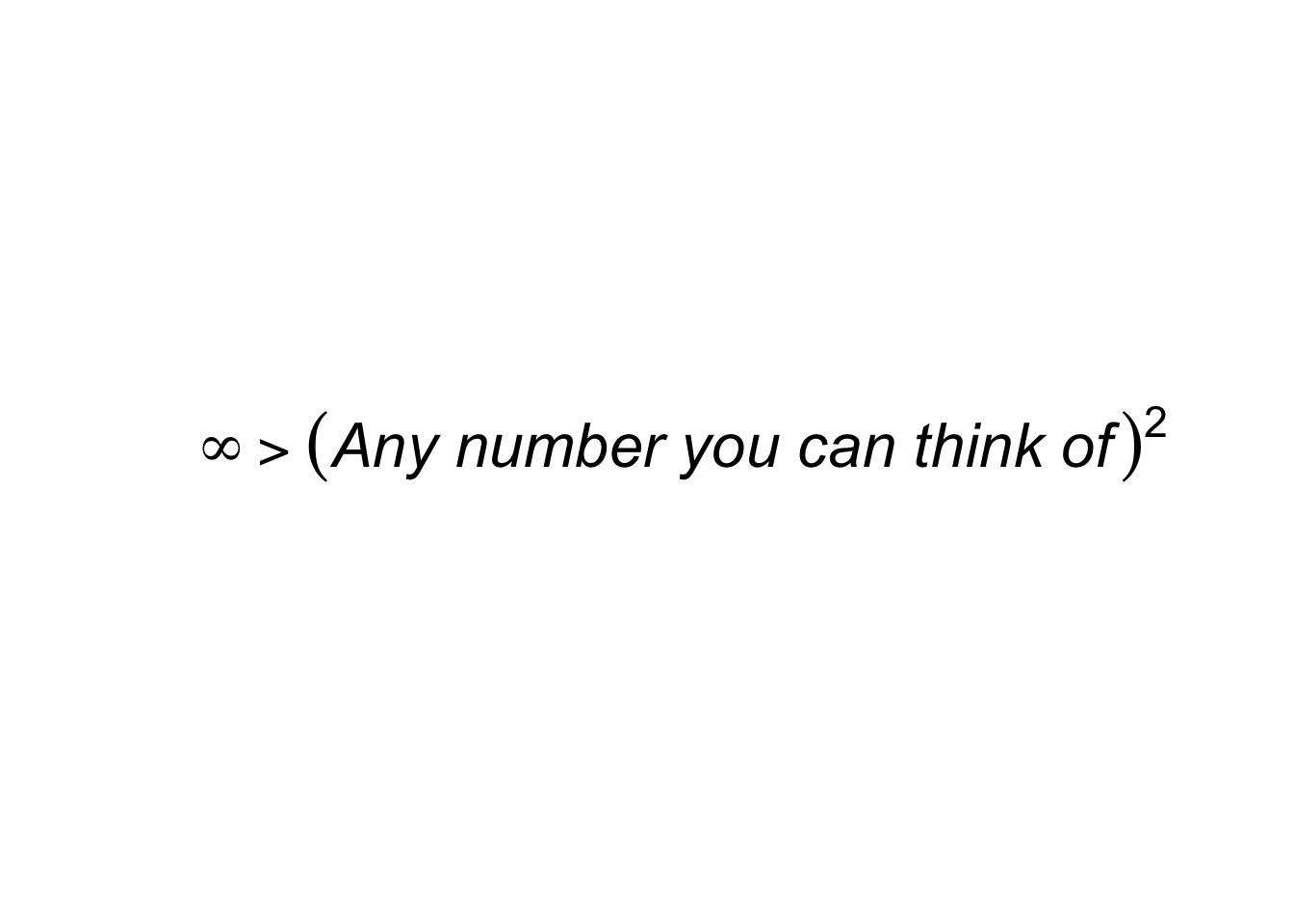

Recursive Plotmath

You can put plotmath within other plotmath expressions by using bquote() or substitute().

first_plotmath  <- bquote(x ^ 2)
second_plotmath <- bquote(y ^ .(first_plotmath))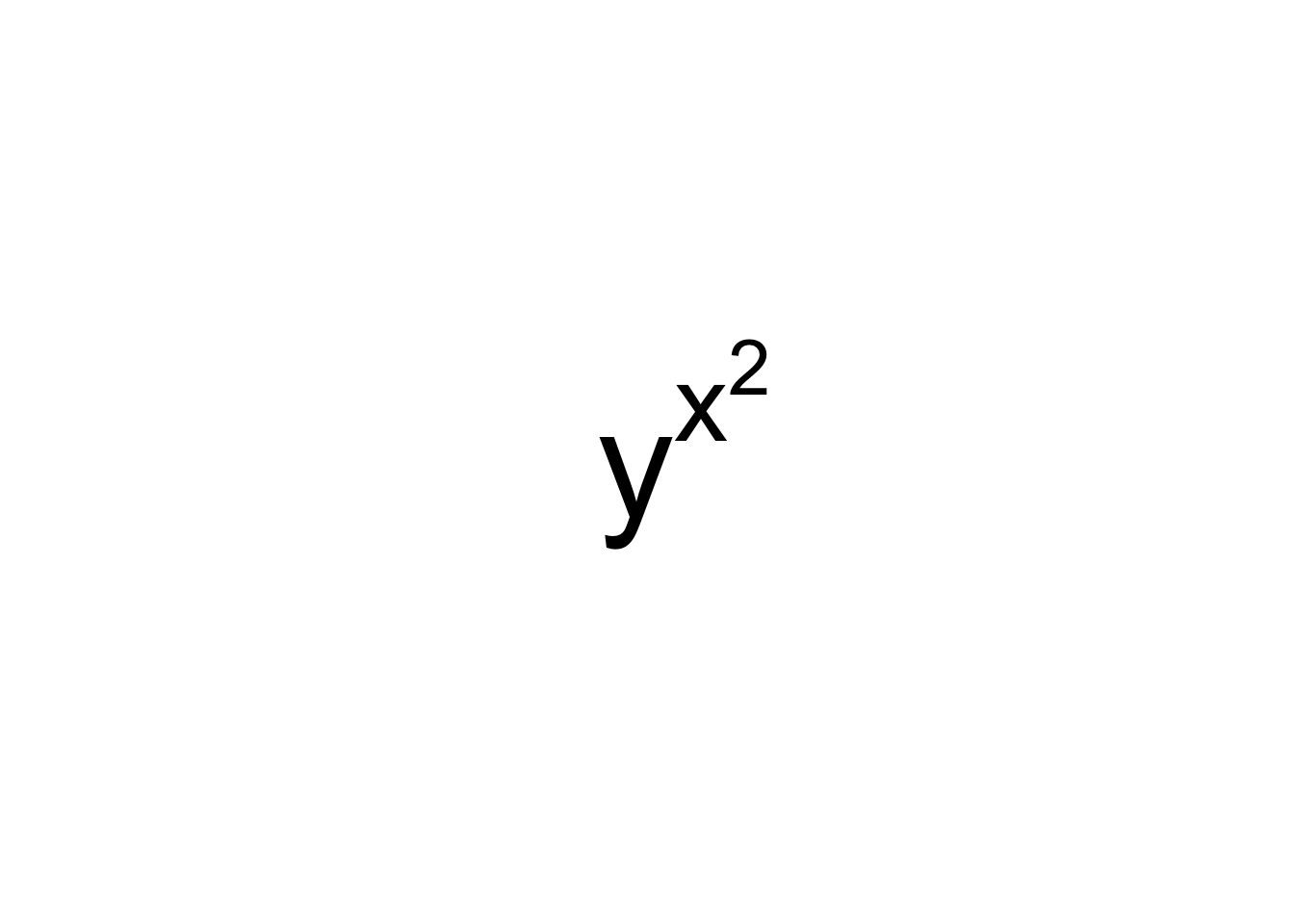

Mega Plotmath

Once we can put plotmath into other plotmath expressions, we can apply the same manipulation over and over to build bigger and bigger structures.

square <- function(x) { bquote(frac(.(x), .(x)) + frac(.(x), .(x))) }

x <- bquote(frac(alpha + beta, gamma - delta))
x <- square(x)
x <- square(x)
x <- square(x)
x <- square(x)
x <- square(x)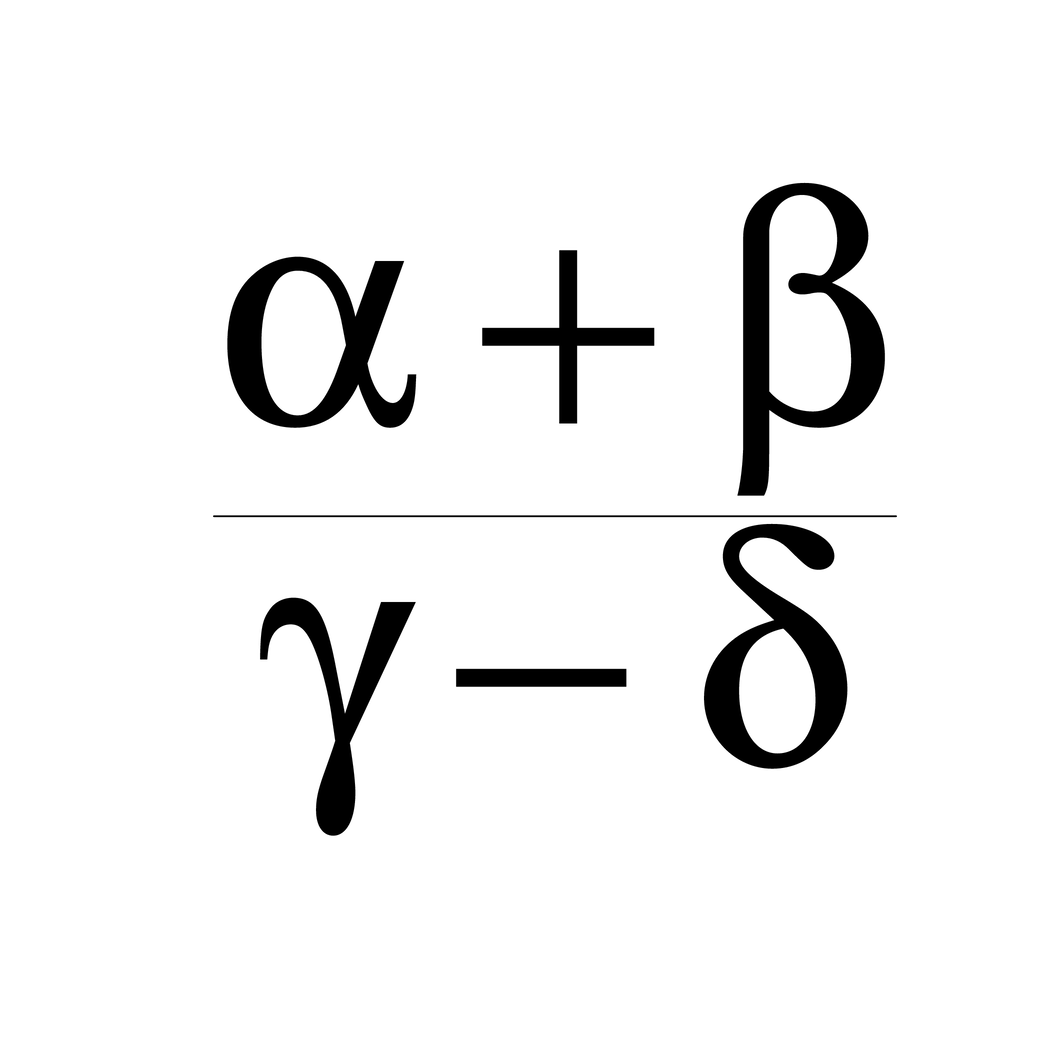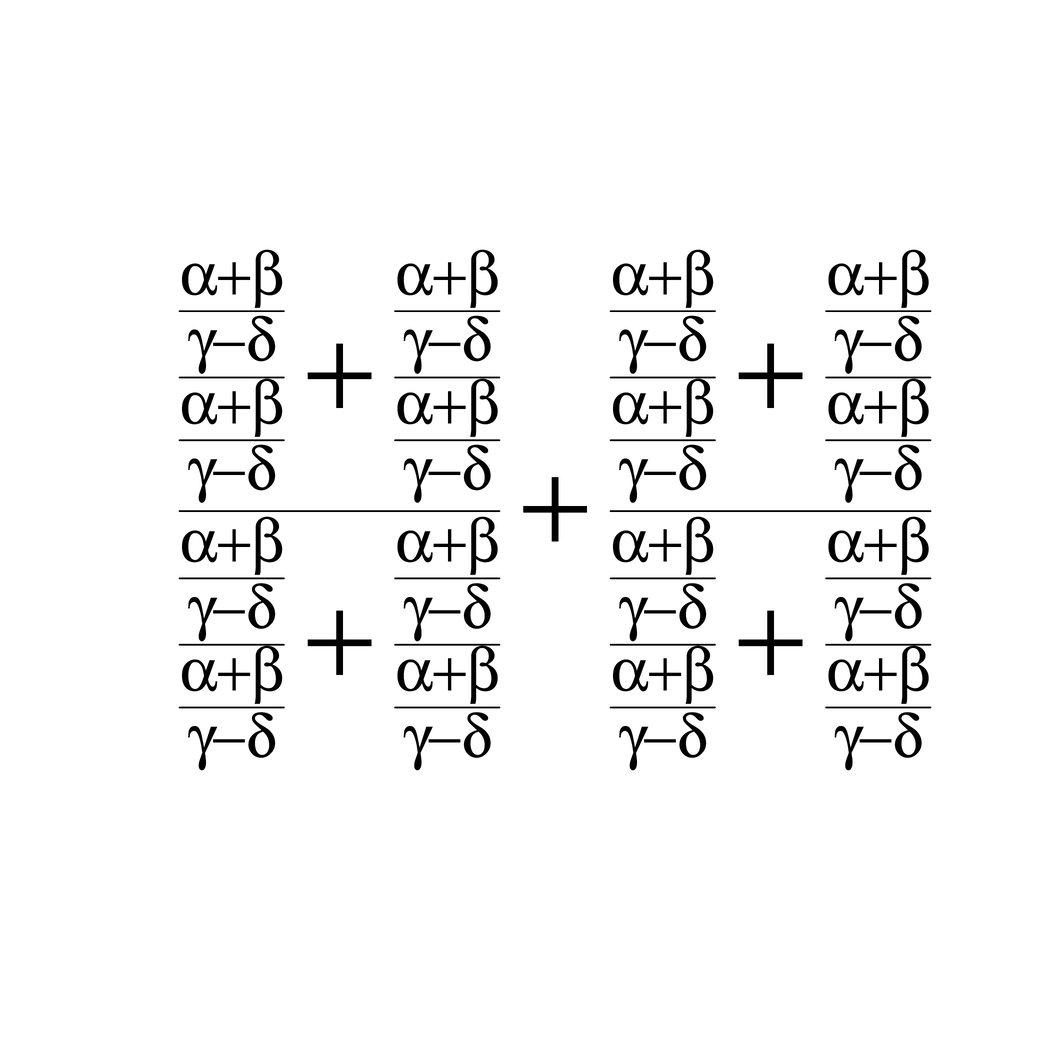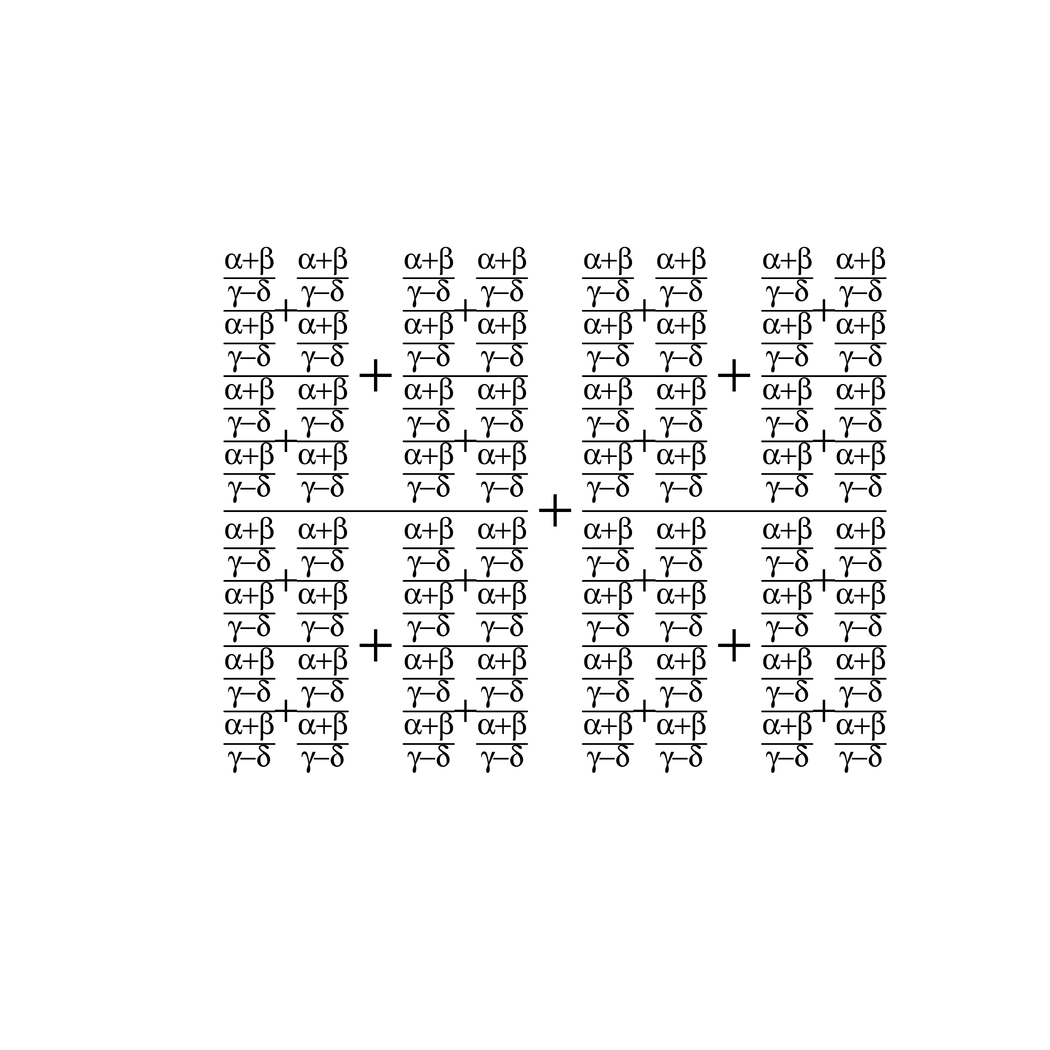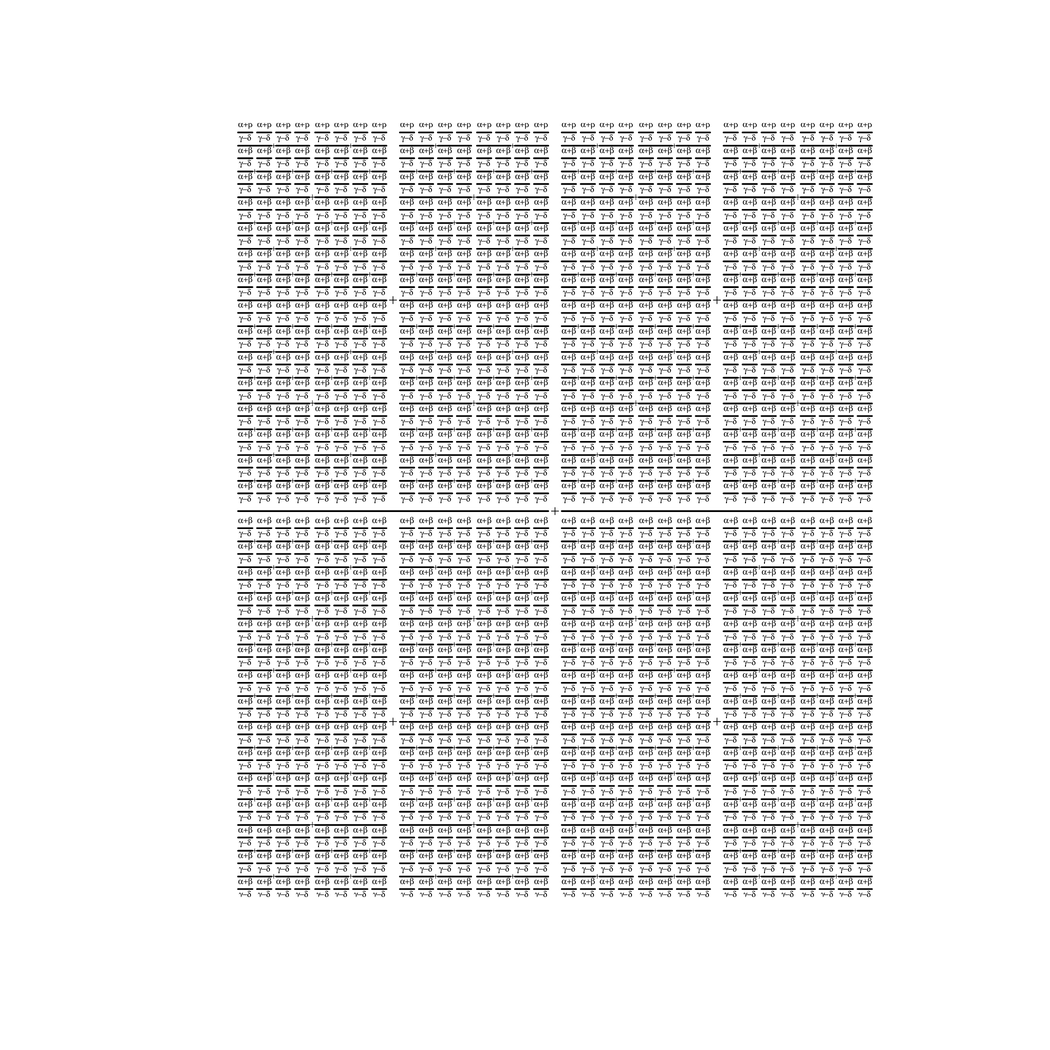

Fractal Plotmath - Sierpinkski triangle

If the iterated plotmath expression contains an offset and a translate then you can create the classic sierpinski triangle.

sierpinski   <- function(x) { bquote(atop(.(x), .(x) * .(x))) }

x <- bquote(alpha^2)
x <- sierpinski(x)
x <- sierpinski(x)
x <- sierpinski(x)
x <- sierpinski(x)
x <- sierpinski(x)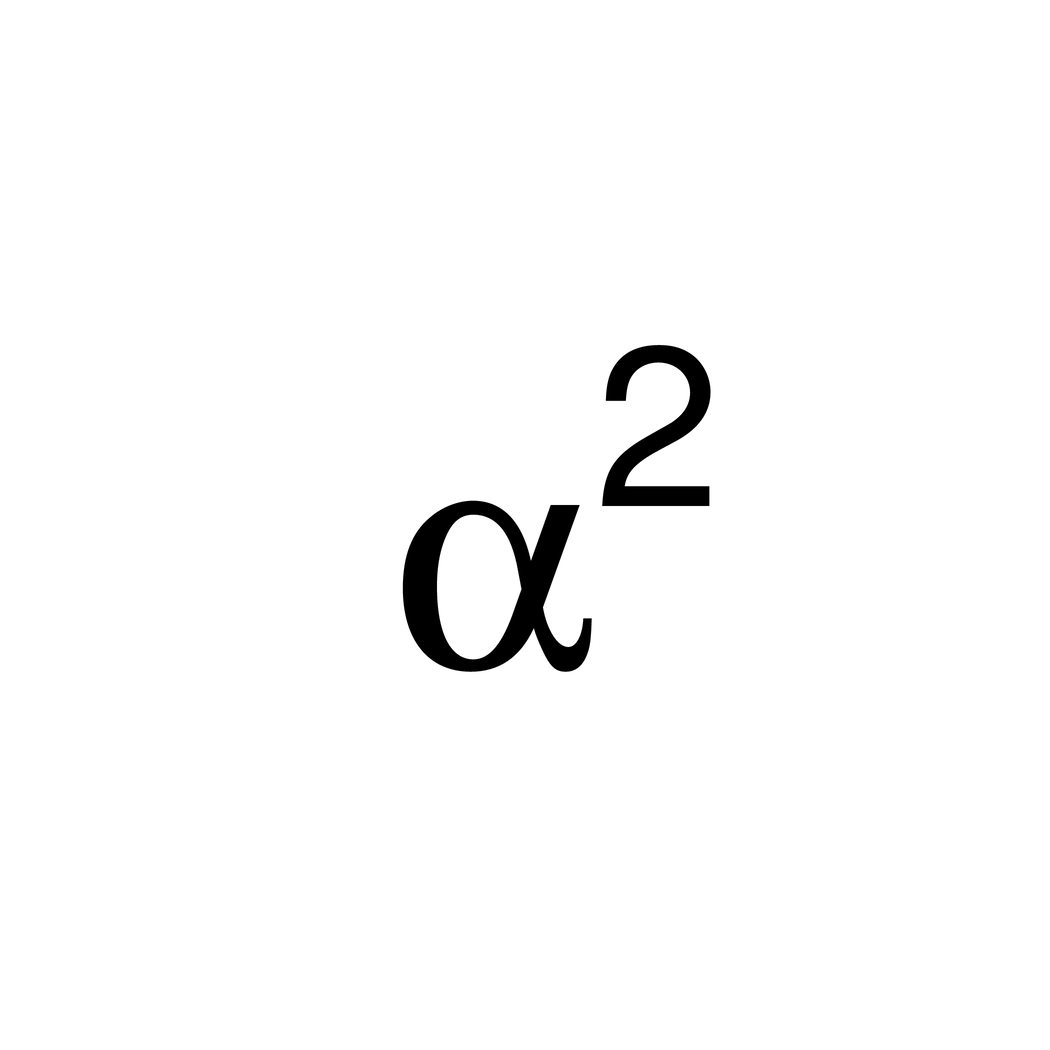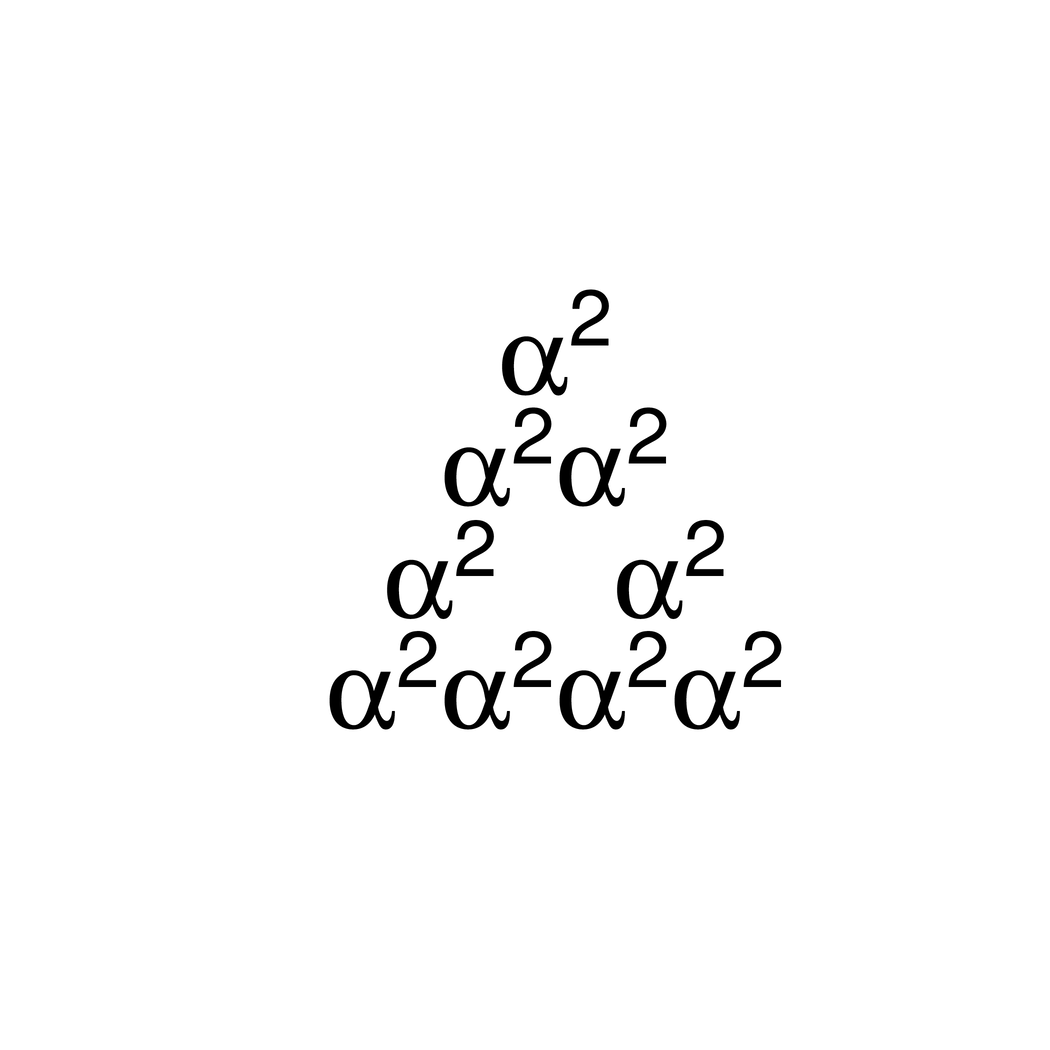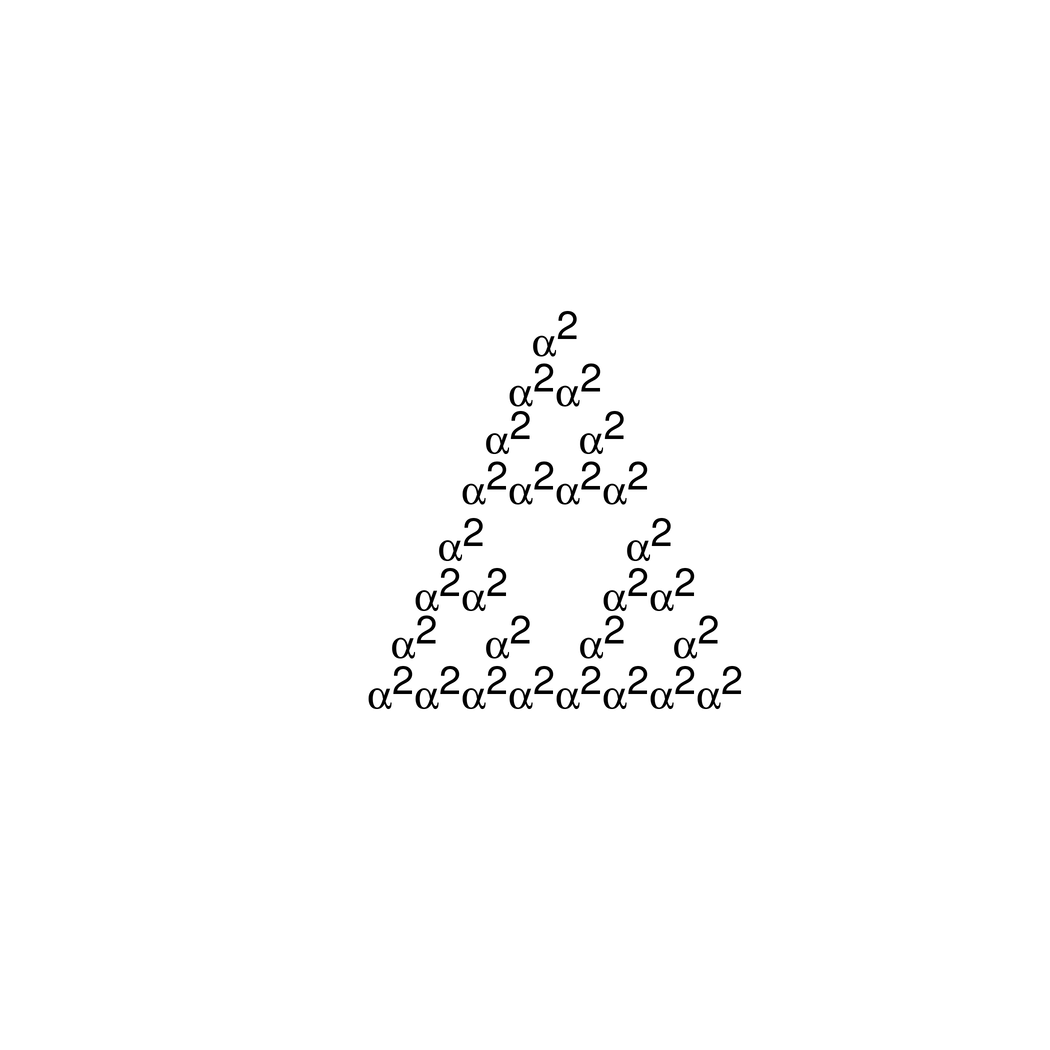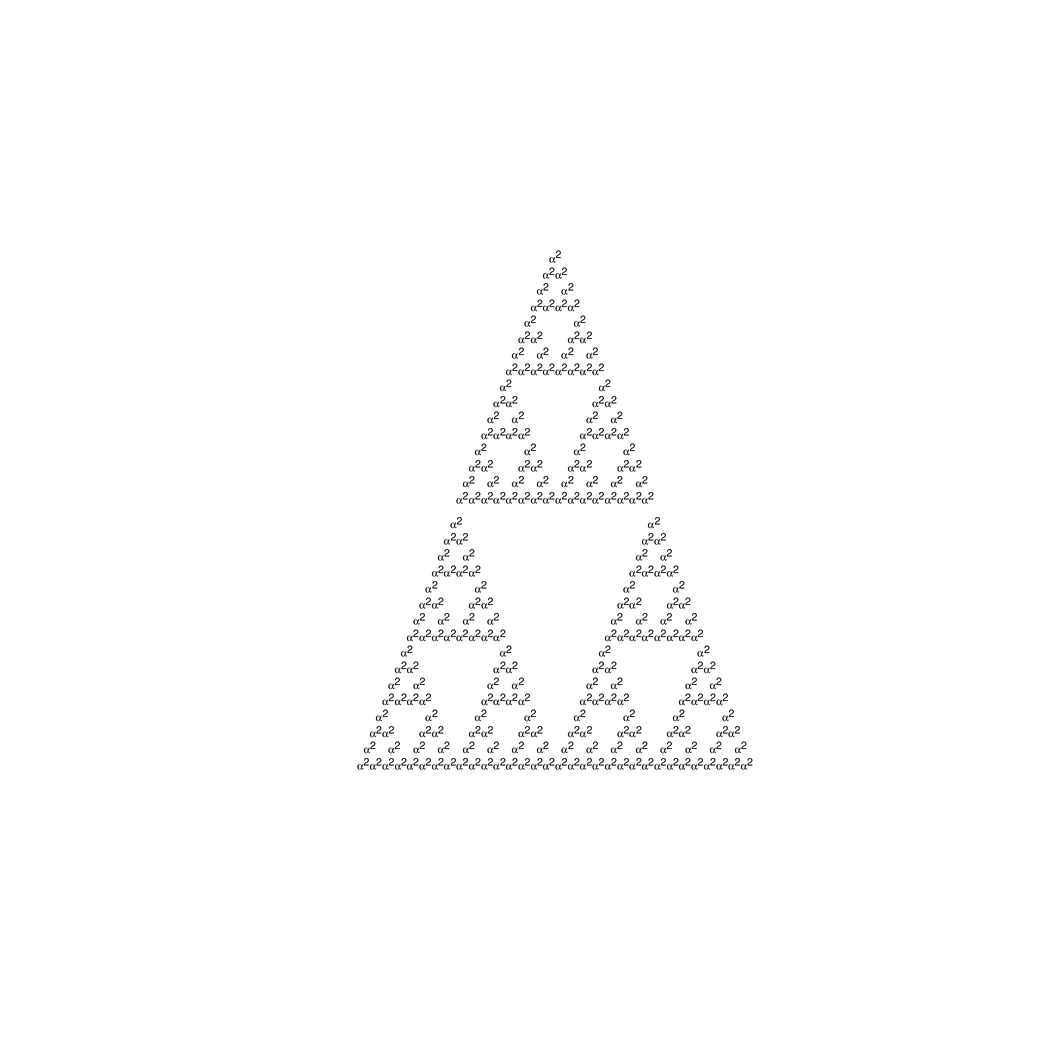

And this is what the plotmath looks like for this sierpinski triangle

atop(atop(atop(atop(atop(alpha^2, alpha^2 * alpha^2), atop(alpha^2, 
    alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * alpha^2)), atop(atop(alpha^2, 
    alpha^2 * alpha^2), atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, 
    alpha^2 * alpha^2)) * atop(atop(alpha^2, alpha^2 * alpha^2), 
    atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
        alpha^2))), atop(atop(atop(alpha^2, alpha^2 * alpha^2), 
    atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
        alpha^2)), atop(atop(alpha^2, alpha^2 * alpha^2), atop(alpha^2, 
    alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * alpha^2)) * 
    atop(atop(alpha^2, alpha^2 * alpha^2), atop(alpha^2, alpha^2 * 
        alpha^2) * atop(alpha^2, alpha^2 * alpha^2))) * atop(atop(atop(alpha^2, 
    alpha^2 * alpha^2), atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, 
    alpha^2 * alpha^2)), atop(atop(alpha^2, alpha^2 * alpha^2), 
    atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
        alpha^2)) * atop(atop(alpha^2, alpha^2 * alpha^2), atop(alpha^2, 
    alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * alpha^2)))), 
    atop(atop(atop(atop(alpha^2, alpha^2 * alpha^2), atop(alpha^2, 
        alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * alpha^2)), 
        atop(atop(alpha^2, alpha^2 * alpha^2), atop(alpha^2, 
            alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * alpha^2)) * 
            atop(atop(alpha^2, alpha^2 * alpha^2), atop(alpha^2, 
                alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
                alpha^2))), atop(atop(atop(alpha^2, alpha^2 * 
        alpha^2), atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, 
        alpha^2 * alpha^2)), atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)) * atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2))) * atop(atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)), atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)) * atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)))) * atop(atop(atop(atop(alpha^2, alpha^2 * 
        alpha^2), atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, 
        alpha^2 * alpha^2)), atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)) * atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2))), atop(atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)), atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)) * atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2))) * atop(atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)), atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)) * atop(atop(alpha^2, alpha^2 * alpha^2), 
        atop(alpha^2, alpha^2 * alpha^2) * atop(alpha^2, alpha^2 * 
            alpha^2)))))