Problem - Finding the intersection of multiple integer vectors
- I want to find the intersection of multiple integer vectors
- Unbounded number of vectors, but usually 4-10
- Unbounded size, but usually 10 to a million elements
- Duplicated elements allowed in output
- Order not important
- Submissions welcomed! (including alternate test sets that demonstrate a
different dominant solution)
Test set
- Benchmarking data:
- 10 vectors
- Varying lengths
- Elements sampled from range (1, 1e5)
- I realise that this benchmarking data ignores the following cases
- a few short vectors
- very long vectors
- vectors already sorted by size
- vectors with large overlap
- vectors with no overlap
set.seed(1)
source <- seq.int(1e5)
a <- sample(source, size=1.0e5, replace=TRUE)
b <- sample(source, size=0.9e5, replace=TRUE)
c <- sample(source, size=0.8e5, replace=TRUE)
d <- sample(source, size=0.7e5, replace=TRUE)
e <- sample(source, size=0.6e5, replace=TRUE)
f <- sample(source, size=0.5e5, replace=TRUE)
g <- sample(source, size=0.4e5, replace=TRUE)
h <- sample(source, size=0.3e5, replace=TRUE)
i <- sample(source, size=0.2e5, replace=TRUE)
j <- sample(source, size=0.1e5, replace=TRUE)
for loop
intersection_0_forloop <- function(...) {
ll <- list(...)
working_set <- ll[[1]]
for (l in ll[-1]) {
working_set <- intersect(working_set, l)
}
working_set
}
sort(unique(intersection_0_forloop(a, b, c, d, e, f, g, h, i)))
[1] 1258 4071 5370 7151 7749 14098 20244 23662 28383 32717 32730 40064
[13] 40376 44214 49955 53971 54336 54986 59242 61623 63523 67816 71673 82711
[25] 82976 83606 86895 90685 91729 92002 95154
Reduce()
- Acculmulate
intersect() vector by vector using Reduce()
- Under the hood, this works identical to the
for loop example above…
- … but it’s much better looking :)
intersection_1_reduce <- function(...) {
Reduce(intersect, list(...))
}
sort(unique(intersection_1_reduce(a, b, c, d, e, f, g, h, i)))
[1] 1258 4071 5370 7151 7749 14098 20244 23662 28383 32717 32730 40064
[13] 40376 44214 49955 53971 54336 54986 59242 61623 63523 67816 71673 82711
[25] 82976 83606 86895 90685 91729 92002 95154
Sort by length and then Reduce()
- Acculmulate
intersect() vector by vector using Reduce()
- Start with the shortest vector first.
- By ensuring that the intermediate result is always as short as possible, it should
reduce the memory allocations.
intersection_2_reduce_sorted <- function(...) {
ll <- list(...)
lens <- vapply(ll, length, integer(1))
ll <- ll[order(lens)]
Reduce(intersect, ll)
}
sort(unique(intersection_2_reduce_sorted(a, b, c, d, e, f, g, h, i)))
[1] 1258 4071 5370 7151 7749 14098 20244 23662 28383 32717 32730 40064
[13] 40376 44214 49955 53971 54336 54986 59242 61623 63523 67816 71673 82711
[25] 82976 83606 86895 90685 91729 92002 95154
Tally vector
- Initialise a
tally vector wtih length equal to the maximum integer across
all the vectors.
- For each element in each vector, increase the
tally for that element by 1.
- Find all counts in the
tally vector which match the number of vectors given.
- This will be increasingly inefficient as
maxval gets larger and larger.
intersection_3_tally <- function(...) {
ll <- list(...)
maxval <- max(vapply(ll, max, integer(1)))
tally <- integer(maxval)
for (elements in ll) {
tally[elements] <- tally[elements] + 1L
}
which(tally == length(ll))
}
sort(unique(intersection_3_tally(a, b, c, d, e, f, g, h, i)))
[1] 1258 4071 5370 7151 7749 14098 20244 23662 28383 32717 32730 40064
[13] 40376 44214 49955 53971 54336 54986 59242 61623 63523 67816 71673 82711
[25] 82976 83606 86895 90685 91729 92002 95154
Rcpp function
- An Rcpp integer-only version of
intersect()
- An R wrapper to go with it.
- side effect: original vectors are sorted numerically.
Rcpp::cppFunction(
"std::vector<int> intersection_rcpp_core(IntegerVector v1, IntegerVector v2) {
std::sort(v1.begin(), v1.end());
std::sort(v2.begin(), v2.end());
std::vector<int> v_intersection;
std::set_intersection(v1.begin(), v1.end(),
v2.begin(), v2.end(),
std::back_inserter(v_intersection));
return v_intersection;
}
")
intersection_4_rcpp <- function(...) {
Reduce(intersection_rcpp_core, list(...))
}
sort(unique(intersection_4_rcpp(a, b, c, d, e, f, g, h, i)))
[1] 1258 4071 5370 7151 7749 14098 20244 23662 28383 32717 32730 40064
[13] 40376 44214 49955 53971 54336 54986 59242 61623 63523 67816 71673 82711
[25] 82976 83606 86895 90685 91729 92002 95154
Benchmark
bm <- bench::mark(
intersection_0_forloop (a, b, c, d, e, f, g, h, i, j),
intersection_1_reduce (a, b, c, d, e, f, g, h, i, j),
intersection_2_reduce_sorted(a, b, c, d, e, f, g, h, i, j),
intersection_3_tally (a, b, c, d, e, f, g, h, i, j),
intersection_4_rcpp (a, b, c, d, e, f, g, h, i, j),
check = FALSE
)
| intersection_0_forloop(a, b, c, d, e, f, g, h, i, j) |
64.17ms |
15.42914 |
10.55MB |
| intersection_1_reduce(a, b, c, d, e, f, g, h, i, j) |
69.37ms |
14.69209 |
10.56MB |
| intersection_2_reduce_sorted(a, b, c, d, e, f, g, h, i, j) |
46.66ms |
21.68236 |
8.24MB |
| intersection_3_tally(a, b, c, d, e, f, g, h, i, j) |
7.41ms |
133.20700 |
3.24MB |
| intersection_4_rcpp(a, b, c, d, e, f, g, h, i, j) |
2.89ms |
339.86518 |
356.72KB |
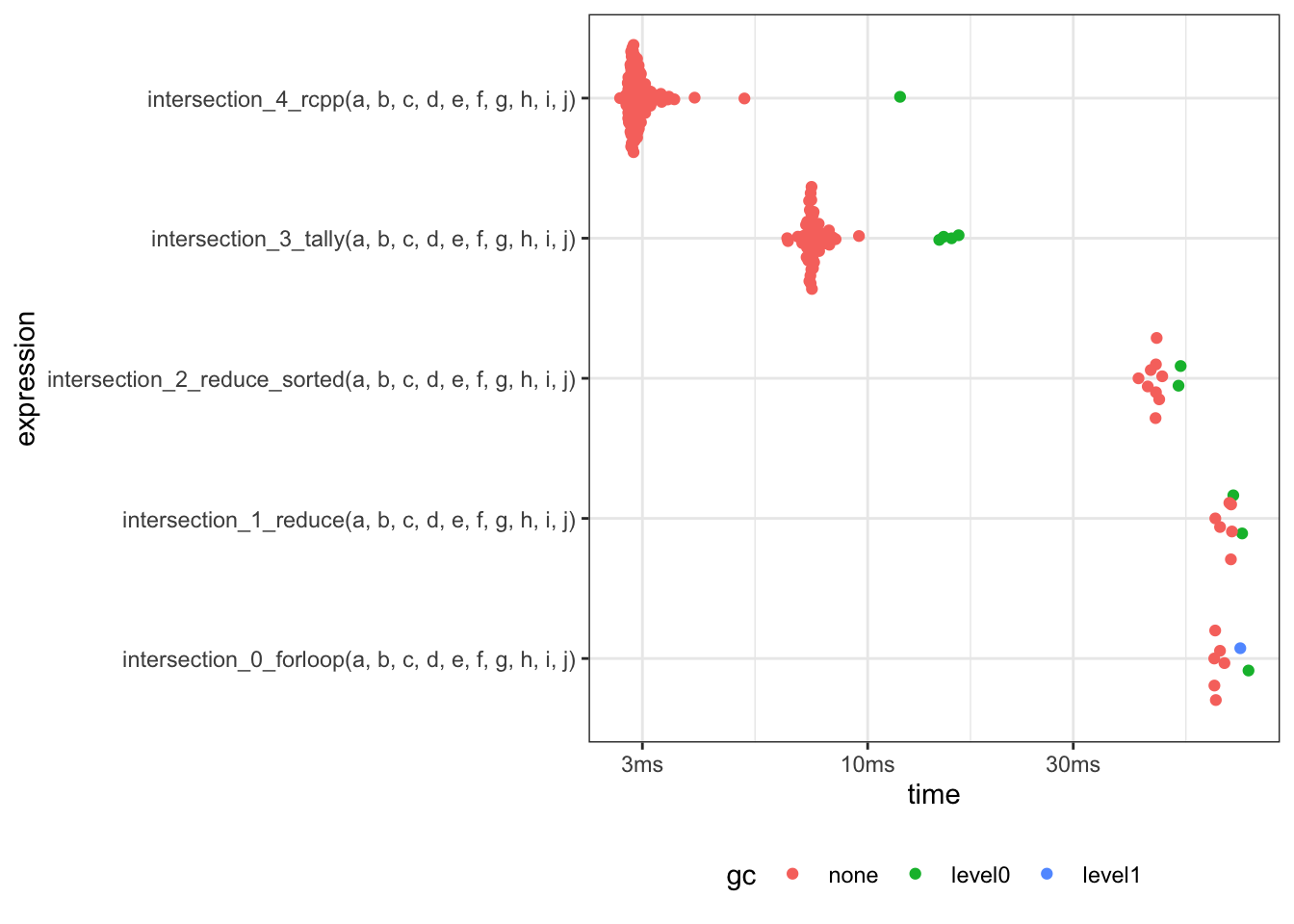
Summary
- Under-the-hood, the
for loop and the Reduce() methods are identical and this
is evidenced by their identical runtimes.
- Sorting input vectors by length results in a 2x speed-up over the base case for
this benchmark example (which is pretty pathological with the vectors in order
of decreasing size)
- Using a tally vector instead of the builtin
intersect() results in a ~9x speedup over the
base case.
Rcpp is clearly the fastest with least memory use.
- This could be extended to be a pure
Rcpp function with the functionality
of the Reduce() done in C++
- Could also implement the tally/memory technique in
Rcpp
- Contributions welcomed!
