Problem
This problem popped up as a necessary step to solving a type of puzzle (which I’ll post about soon).
- From the set of all positive (non-zero) integers, find all the sequences of the specified length which have the given sum.
- Need all orderings
- sums usually range from 10 to 30
- lengths usually range from 2 to 10
Example: All the length=3 vectors which sum to 5 (one sequence per row)
[,1] [,2] [,3]
[1,] 1 1 3
[2,] 1 2 2
[3,] 1 3 1
[4,] 2 1 2
[5,] 2 2 1
[6,] 3 1 1Naive solution - generate all sequences, then filter
- Use expand grid to expand all possible sequences.
- Then filter where
rowSums()is equal to the requiredtarget_sum - Scales really badly as the sum and length targets get bigger
find_sequences_with_sum_naive <- function(target_sum, target_length) {
res <- do.call(expand.grid, replicate(n=target_length, seq(target_sum - target_length + 1L), simplify = FALSE))
res[rowSums(res) == target_sum,]
}
find_sequences_with_sum_naive(5, 3) Var1 Var2 Var3
3 3 1 1
5 2 2 1
7 1 3 1
11 2 1 2
13 1 2 2
19 1 1 3Iterative solution with back-tracking
- build up vectors one digit at a time
- stop if the required length or sum is exceeded and try a different sequence
find_sequences_with_sum <- function(target_sum, target_length, current_vec=c(), N=0L, S=0L) {
stopifnot(target_sum >= target_length)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# If we're at the right length, have we found a solution?
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
if (N == target_length) {
if (S == target_sum) {
return(list(current_vec))
} else {
return()
}
}
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Limit the choices in the next iteration to just ones that are possible
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
max_choice <- (target_sum - S) - (target_length - N) + 1L
choices <- 1:max_choice
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# For each choice, add it to the current_vec and see if that is a pathway
# to a solution
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
solutions <- list()
for (new_val in choices) {
this_solution <- find_sequences_with_sum(target_sum, target_length, c(current_vec, new_val), N=N+1L, S=S+new_val)
solutions <- c(solutions, this_solution)
}
solutions
}
do.call(rbind, find_sequences_with_sum(5, 3)) [,1] [,2] [,3]
[1,] 1 1 3
[2,] 1 2 2
[3,] 1 3 1
[4,] 2 1 2
[5,] 2 2 1
[6,] 3 1 1Quick benchmark
- For small problems, results are roughly similar.
Small example
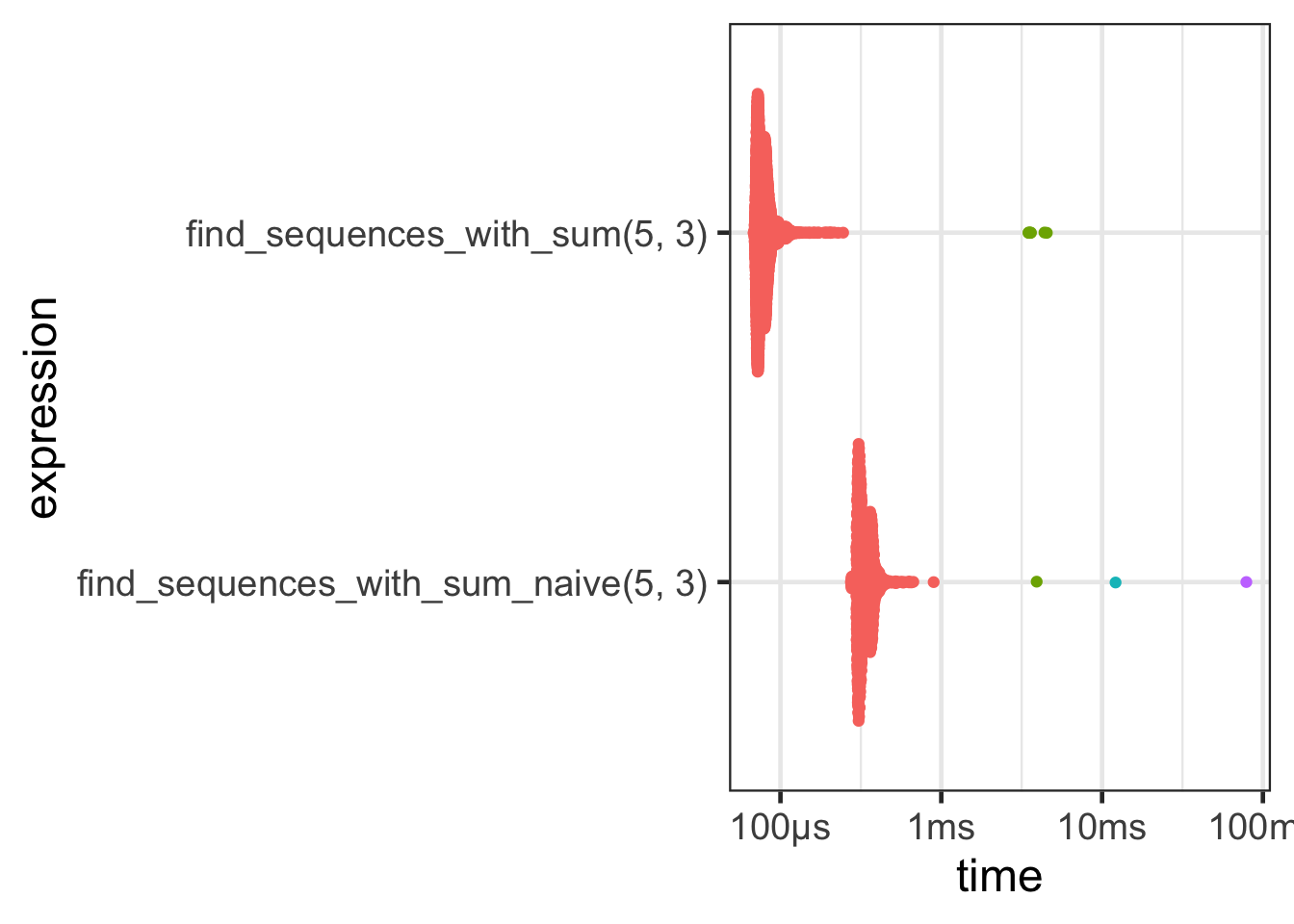
| expression | median | itr/sec | mem_alloc |
|---|---|---|---|
| find_sequences_with_sum_naive(5, 3) | 321.3µs | 2956.288 | 64.9KB |
| find_sequences_with_sum(5, 3) | 77.4µs | 12581.641 | 0B |
Medium-sized example
- Once the problem becomes moderately large, the back-tracking solution (to no-one’s surprise) is faster and uses less memory.
- in this case, ~3x as fast and ~1000x less memory
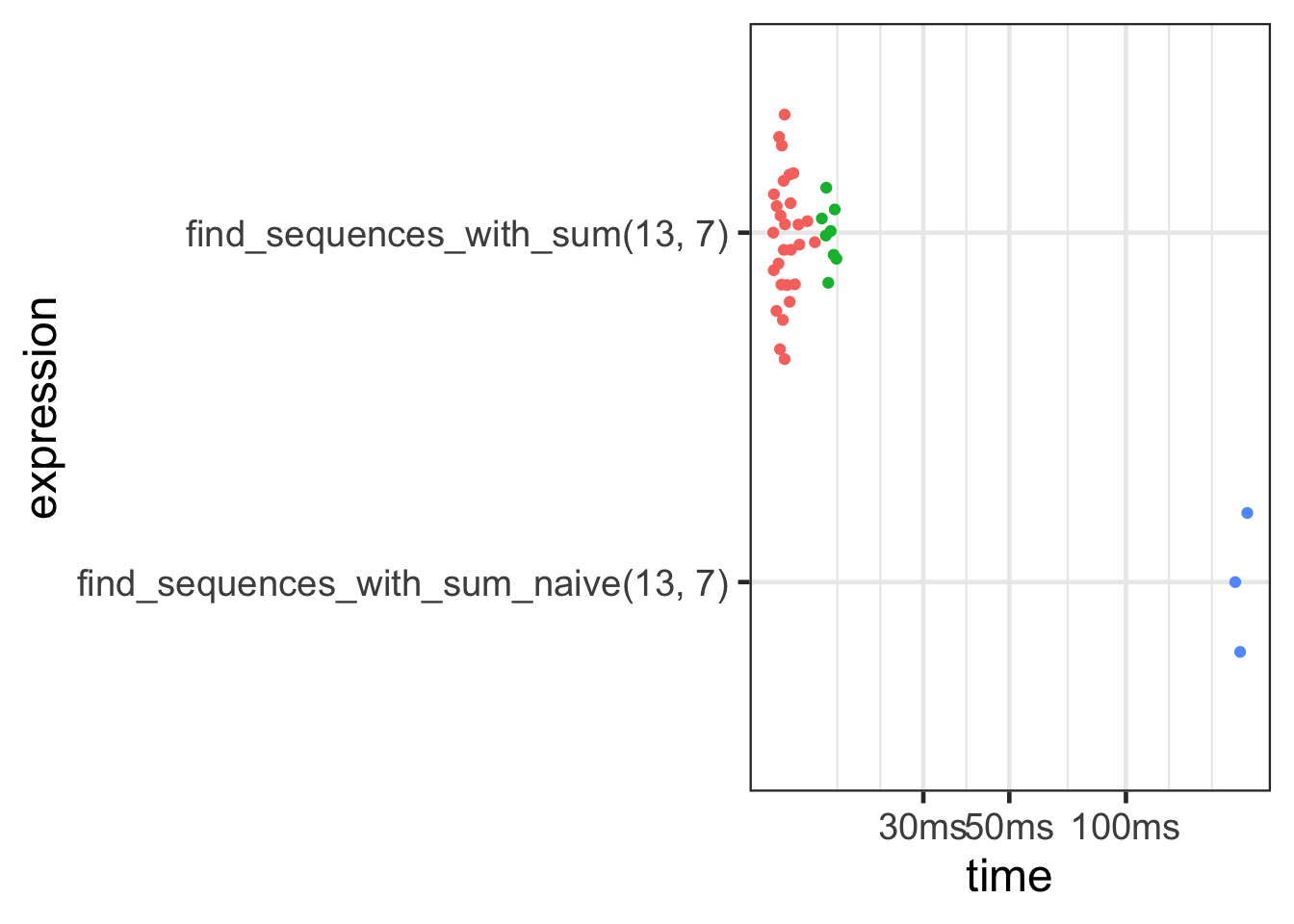
| expression | median | itr/sec | mem_alloc |
|---|---|---|---|
| find_sequences_with_sum_naive(13, 7) | 197.1ms | 5.048857 | 104MB |
| find_sequences_with_sum(13, 7) | 13.4ms | 70.538884 | 142KB |
Summary
- Use the back-tracking solution