Nonograms - Make Run-Length Encoding Fun Again
Nonograms are picture logic puzzles in which cells in a grid must be colored or left blank according to numbers at the side of the grid to reveal a hidden picture.
That is, the numbers on the side of the image (the clues) are the run-length encoding of the filled-in squares for each row and column.
By simultaneously satisfying the clues for the rows and columns, a picture is revealed!

In this short series of posts I will:
- Introduce the nonogram package
- Show how to make nonograms by hand, or from an existing image
- Describe the solution techniqe behind the package
The nonogram package
The nonogram package contains tools for plotting, solving and creating nonogram puzzles.
You can install nonogram from github with:
# install.packages("devtools")
devtools::install_github("coolbutuseless/nonogram")Basic example
This is a basic example which shows you how to plot and solve a simple puzzle.
For this example I’ll be using one of the puzzles supplied in the package.
Use one of the puzzle strings in the package
There are 2 lists of puzzles in the package:
puzzle_string_examples- 5 puzzles. Used during development.puzzle_string_library- ~4000 puzzles. Not tested.
puzzle_string <- puzzle_string_examples[['duck']]
puzzle <- convert_puzzle_string_to_puzzle(puzzle_string)Puzzle and Puzzle String representation
- The
puzzle stringrepresentation is a ‘human-friendly’ version of a puzzle - The actual
puzzlerepresentation is a list in R
> puzzle_string3:2,1:3,2:2,2:6:1,5:6:1:2-1,2:3,1:1,5:7,1:5:3:4:3
> puzzlelist(row_clues = list(3L, 2:1, 3:2, c(2L, 2L), 6L, c(1L, 5L),
6L, 1L, 2L), col_clues = list(1:2, c(3L, 1L), c(1L, 5L),
c(7L, 1L), 5L, 3L, 4L, 3L))Plot the unsolved puzzle
create_puzzle_plot(puzzle, title="Duck")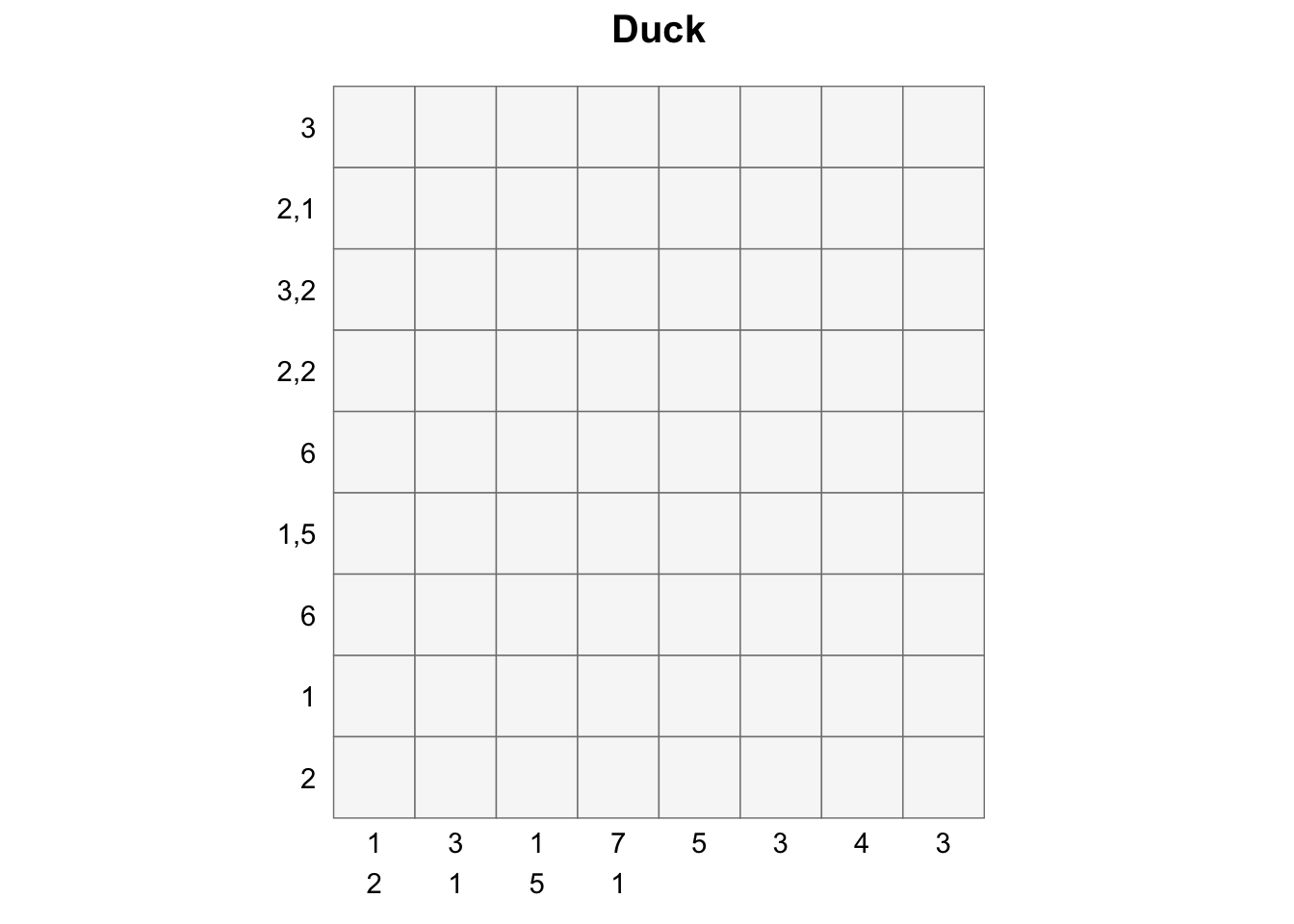
Solve the puzzle
solution_matrix <- solve_puzzle(puzzle)
solution_matrix [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 0 1 1 1 0 0 0 0
[2,] 1 1 0 1 0 0 0 0
[3,] 0 1 1 1 0 0 1 1
[4,] 0 0 1 1 0 0 1 1
[5,] 0 0 1 1 1 1 1 1
[6,] 1 0 1 1 1 1 1 0
[7,] 1 1 1 1 1 1 0 0
[8,] 0 0 0 0 1 0 0 0
[9,] 0 0 0 1 1 0 0 0Plot the solved puzzle
create_puzzle_plot(puzzle, solution_matrix, title="Duck")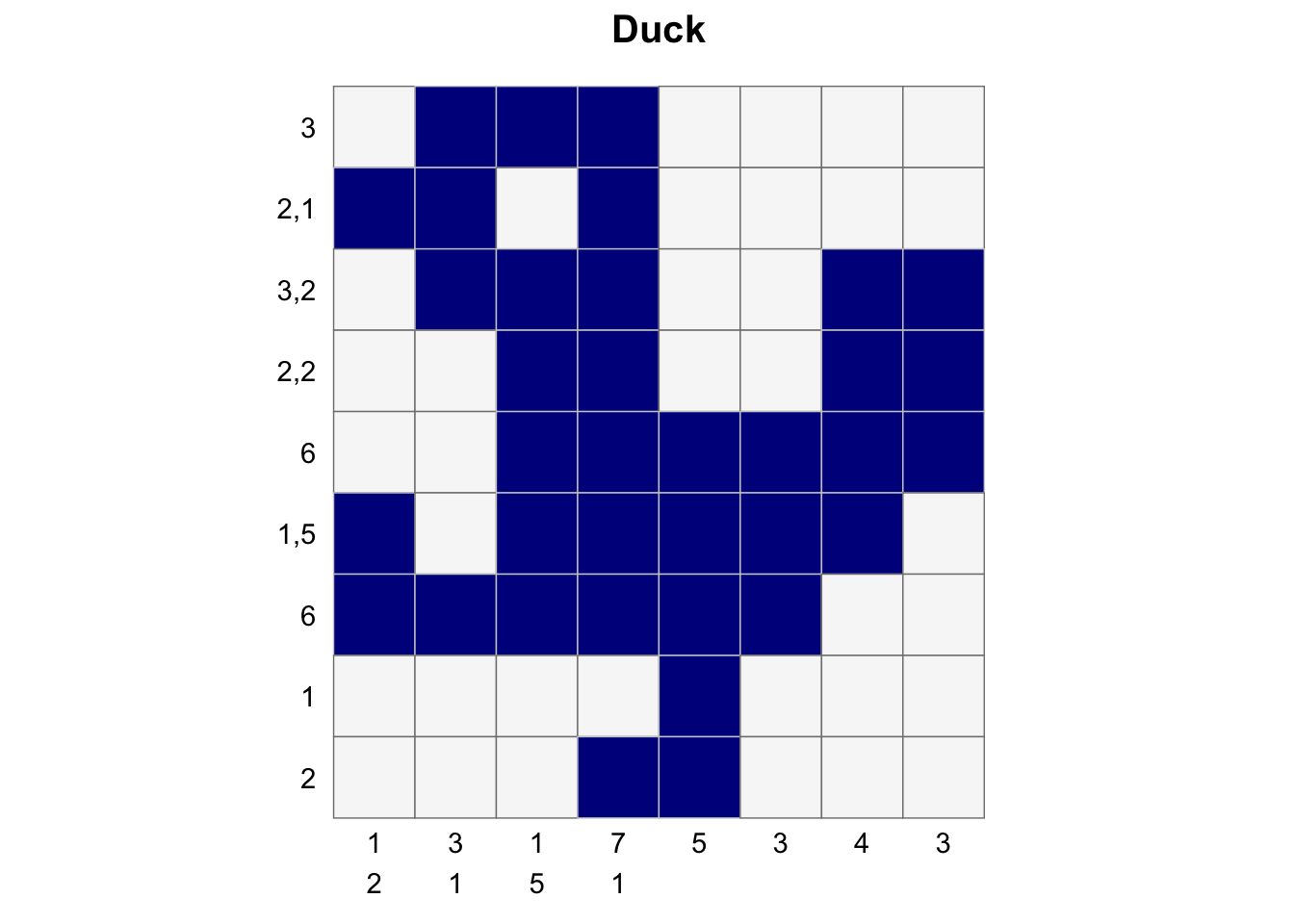
Another example with verbose output of stats and timings
Another example of solving a nonogram is shown below, this time verbose mode
is enabled and you can see the following:
- It takes 0.02 seconds to generate the possible pattern sets for all the clues
- Initially there are 5.8x10^39 combinations of row patterns to try.
- By doing filtering, we bring this down to 1 - which means we’ve solved the puzzle!
- Doing that filtering took 0.01 seconds.
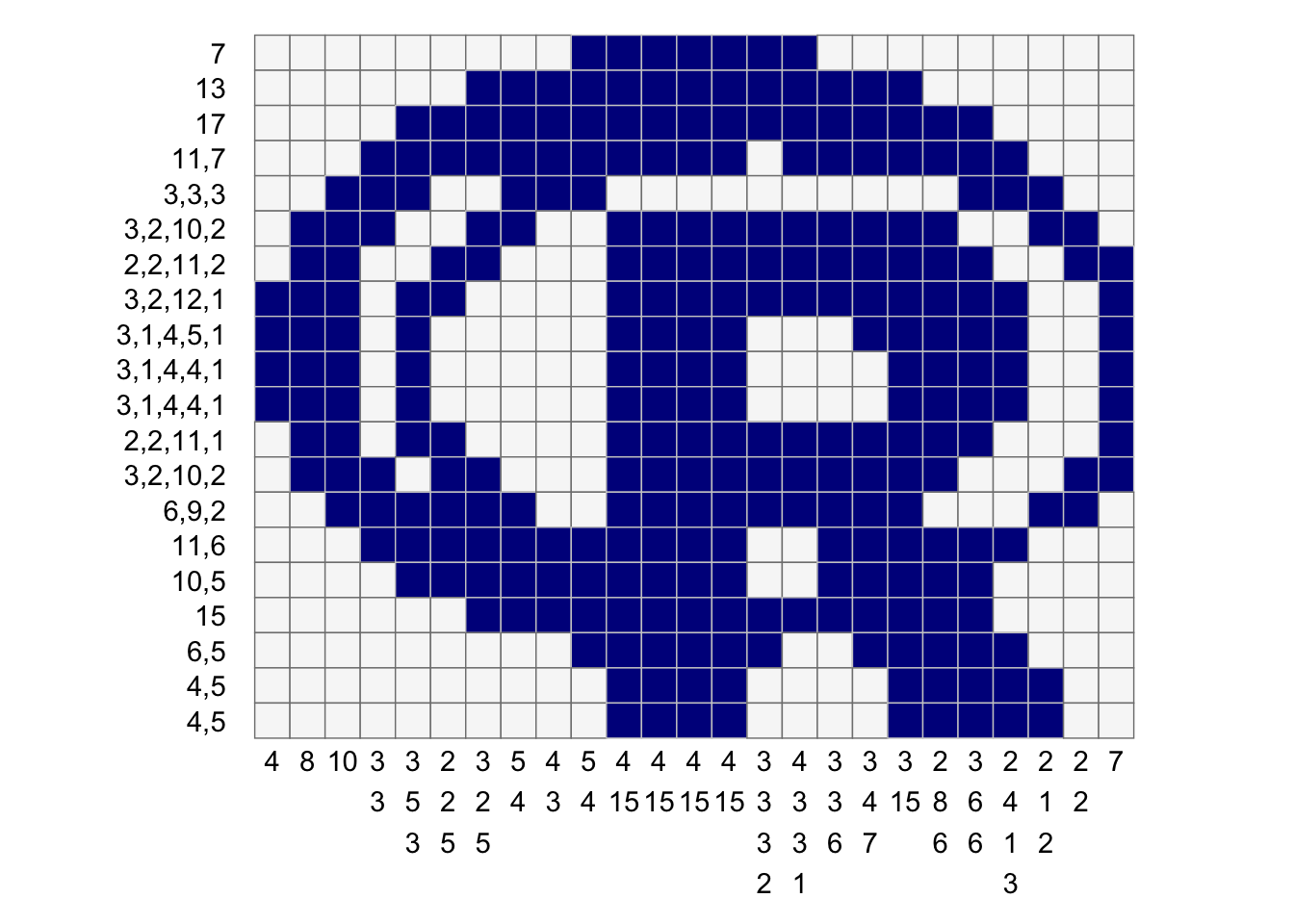
puzzle <- nonogram::puzzle_string_examples[['R']]
puzzle
[1] "7:13:17:11,7:3,3,3:3,2,10,2:2,2,11,2:3,2,12,1:3,1,4,5,1:3,1,4,4,1:3,1,4,4,1:2,2,11,1:3,2,10,2:6,9,2:11,6:10,5:15:6,5:4,5:4,5-4:8:10:3,3:3,5,3:2,2,5:3,2,5:5,4:4,3:5,4:4,15:4,15:4,15:4,15:3,3,3,2:4,3,3,1:3,3,6:3,4,7:3,15:2,8,6:3,6,6:2,4,1,3:2,1,2:2,2:7"
puzzle %>%
nonogram::solve_puzzle(verbose = TRUE) %>%
nonogram::create_puzzle_plot(puzzle, ., show_clues=TRUE)
------------------------------------------------------------
Creating all possible pattern sets. This can take up to a minute (and lots of ram) for some puzzles ...
Creation of all possible pattern sets from the given clues: 0.02 seconds
Starting (Row) x (Column) combinations: 5.8e+39 x 1.21e+37
Filtered (Row) x (Column) combinations: 1 x 1
Total solution time: 0.01 seconds
------------------------------------------------------------
Future
Possible ideas:
- refactor the function which generates all possible patterns so that it can be memoised.
- then re-write
memoise::memoiseto allow memory limits on cacheing
- then re-write
- Try an alternate solution strategy which doesn’t involve the up-front creation of all possible pattern sets - this is a real memory/cpu drain.
Appendix
Nonograms are also known by many other names, including Paint by Numbers, Griddlers, Pic-a-Pix, Picross, PrismaPixels, Pixel Puzzles, Crucipixel, Edel, FigurePic, Hanjie, HeroGlyphix, Illust-Logic, Japanese Crosswords, Japanese Puzzles, Kare Karala!, Logic Art, Logic Square, Logicolor, Logik-Puzzles, Logimage, Oekaki Logic, Oekaki-Mate, Paint Logic, Picture Logic, Tsunamii, Paint by Sudoku and Binary Coloring Books.