Attempt 1 - runif()

My first attempt using runif() to generate any possible number between 0 and the maximum double was never going to work:

rand_uniform <- function(N) {
  runif(N, min = 0, max = .Machine$double.xmax)
}

rand_uniform(10)

 [1] 4.773031e+307 6.689646e+307 1.029815e+308 1.632679e+308 3.625622e+307
 [6] 1.615029e+308 1.698236e+308 1.187912e+308 1.130954e+308 1.110728e+307

Given that the maximum double value on R is approx 2x10^308:

• 50% of all numbers in the range [0, max_double] are above 1x10^308
• 99% of all numbers in the range [0, max_double] are above 2x10^306

So 99.99% of all numbers sampled from a uniform distribution in the range [0, max_double] will be above 2x10^304.

This is never going to give me the diversity of floating point numbers I wanted.

Also, runif() will never generate an NA or Inf value.

Attempt 2 - random magnitude and significand in base 10

Separately draw random numbers for the leading part and exponential part of the double

rand_power10 <- function(N) {
  runif(N, -1, 1) * 10^runif(N, -308, 308)
}

rand_power10(10)

 [1] -3.530508e+267 -3.094719e-178   1.009171e+93 -5.093762e-232  2.188117e-144
 [6]  -3.229847e-73  7.712072e-301   3.498596e-73 -1.287197e+227   2.507201e-99

• Gives a better spread of random doubles
• Not sure that it will ever generate NA or Inf
• Misses out some numbers - e.g. 1.5 x 10^308 will never be output by this method

Attempt 3 - random magnitude and significand in base 2

Separately draw random numbers for the leading part and exponential part of the double, but do this as powers of 2, no powers of 10

rand_power2 <- function(N) {
  runif(N, -1, 1) * 2^runif(N, -1024, 1024)
}

rand_power2(10)

 [1] -2.635011e+196   9.186218e+89 -3.482499e+172  -3.126403e+32   1.375545e+18
 [6]  8.286859e+177  7.923594e-295  -7.186193e-15  7.487349e+142 -1.174630e+118

• Gives a great spread of random doubles
• I think this covers the entire range of values
• Not sure that it will ever generate NA or Inf

Attempt 4 - Generate 64 random bits - 1 bit at atime

Generate any possible 64-bit pattern and cast it to a double precision floating points value.

rand_bits1 <- function(N) {
  readBin(
    packBits(
      sample(as.raw(c(0, 1)), 64 * N, replace = TRUE),
      type = 'raw'
    ),
    what = 'double',
    n    = N
  )
}

rand_bits1(10)

 [1] -1.764955e-298 -2.887630e+176 -1.333649e+299  3.632060e-292   5.835171e-46
 [6] -1.699497e-298  1.461211e-180 -1.370493e-195  5.631333e-256 -1.145778e-215

• Guaranteed to be able to generate every possible 64bit number
• Can generate NA and Inf

Attempt 5 - Generate 64 random bits - 8 bits at a time

Generate any possible 64-bit pattern and cast it to a double precision floating points value.

rand_bits8 <- function(N) {
  readBin(
    sample(as.raw(0:255), N * 8, replace = TRUE),
    what = 'double',
    n    = N
  )
}

rand_bits8(10)

 [1] -5.384031e+226  -4.136980e+04  4.671568e+278 -1.640025e-283   1.392010e-49
 [6]  7.343209e+243  -3.141708e-65 -2.390032e+198 -2.806815e-299  3.123026e+131

• Guaranteed to be able to generate every possible 64bit number
• Can generate NA and Inf

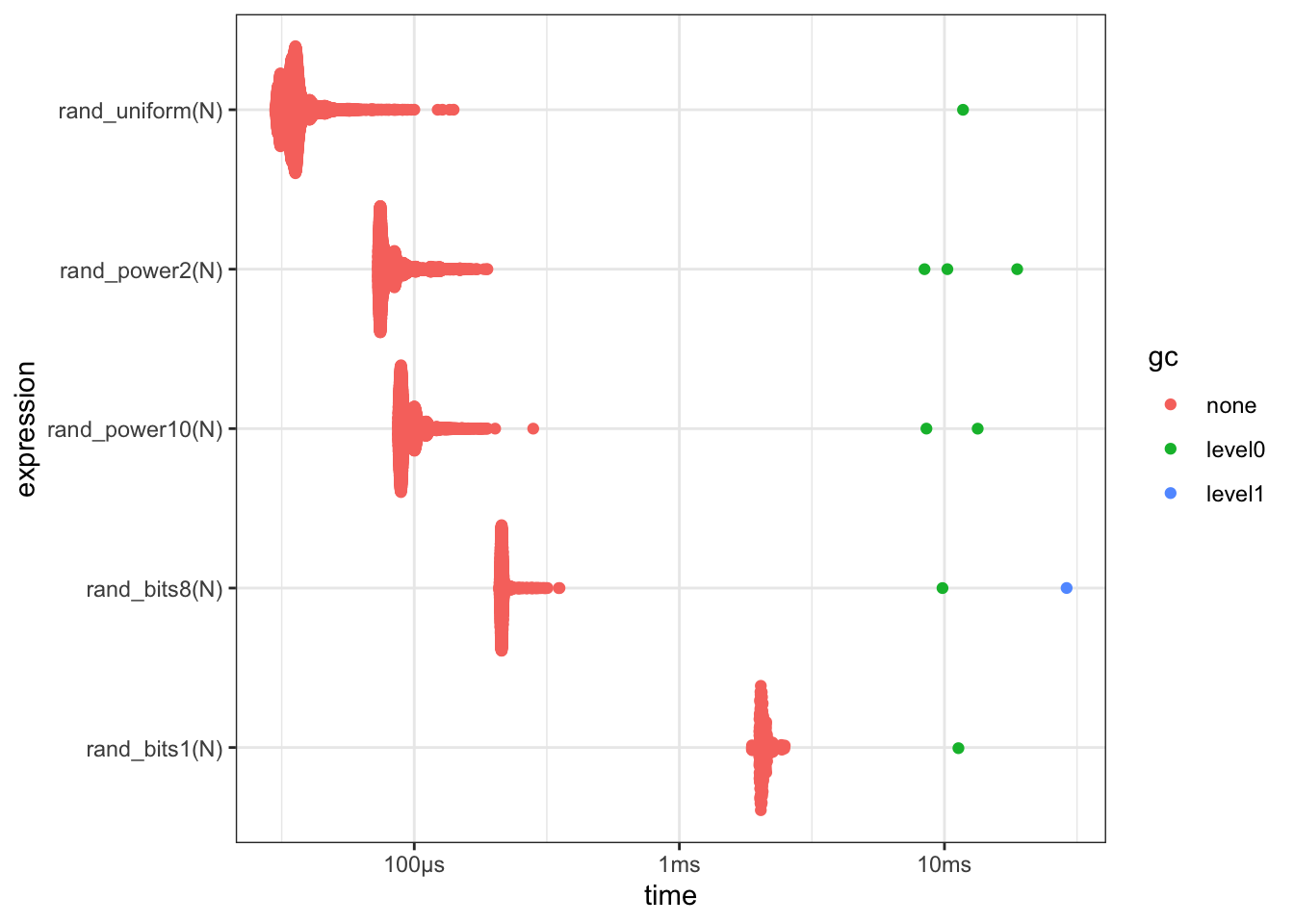
Benchmark

Quick benchmark of the various methods