A mini-exploration of the quality R’s random number generators.
In general, we want pseudo-random number generators (PRNGs) which have (among other things) 2 key properties:
- They should be random
- They should be fast
There are other considerations (e.g. period, availability of multiple streams, jump-aheads etc), but I’m not going there (nor am I considering cryptographic security).
R’s built-in PRNGs
R has 7 built-in PRNGs. These are accessible by calling RNGkind(name) to
switch the backend to use a particular PRNG. The user-facing code
remains the same e.g. runif(), rnorm()
- Mersenne-Twister
- The default PRNG in R
- Also known as: MT19937
- Developed by: Matsumoto and Nishimura, 1997
- Wichmann-Hill
- A combined linear congruential generator (LCG)
- Developed by: Wichman and Hill, 1982
- Marsaglia-Multicarry
- Developed by: Marsaglia, 1997
- Super-Duper
- Developed by: Marsaglia in the 70s
- Knuth-TAOCP-2002
- generalized feedback shift-register generator (GFSR) using lagged Fibonacci sequences
- Developed by: Knuth, 2002
- Knuth-TAOCP
- Another GFSR using using lagged Fibonacci sequences
- Developed by: Knuth, 1997
- L’Ecuyer-CMRG
- A combined multiple recursive generator
- Developed by: L’Ecuyer, 1999
- Defined in this paper Good Parameters and Implementations for Combined Multiple Recursive Random Number Generators (pdf)
- Also known as: MRG32ka
Testing built-in PRNGs for quality
A 2007 paper which reviews many PRNGs and tests then for quality is L’Ecuyer’s TestU01: A C Library for Empirical Testing of Random Number Generators (pdf)
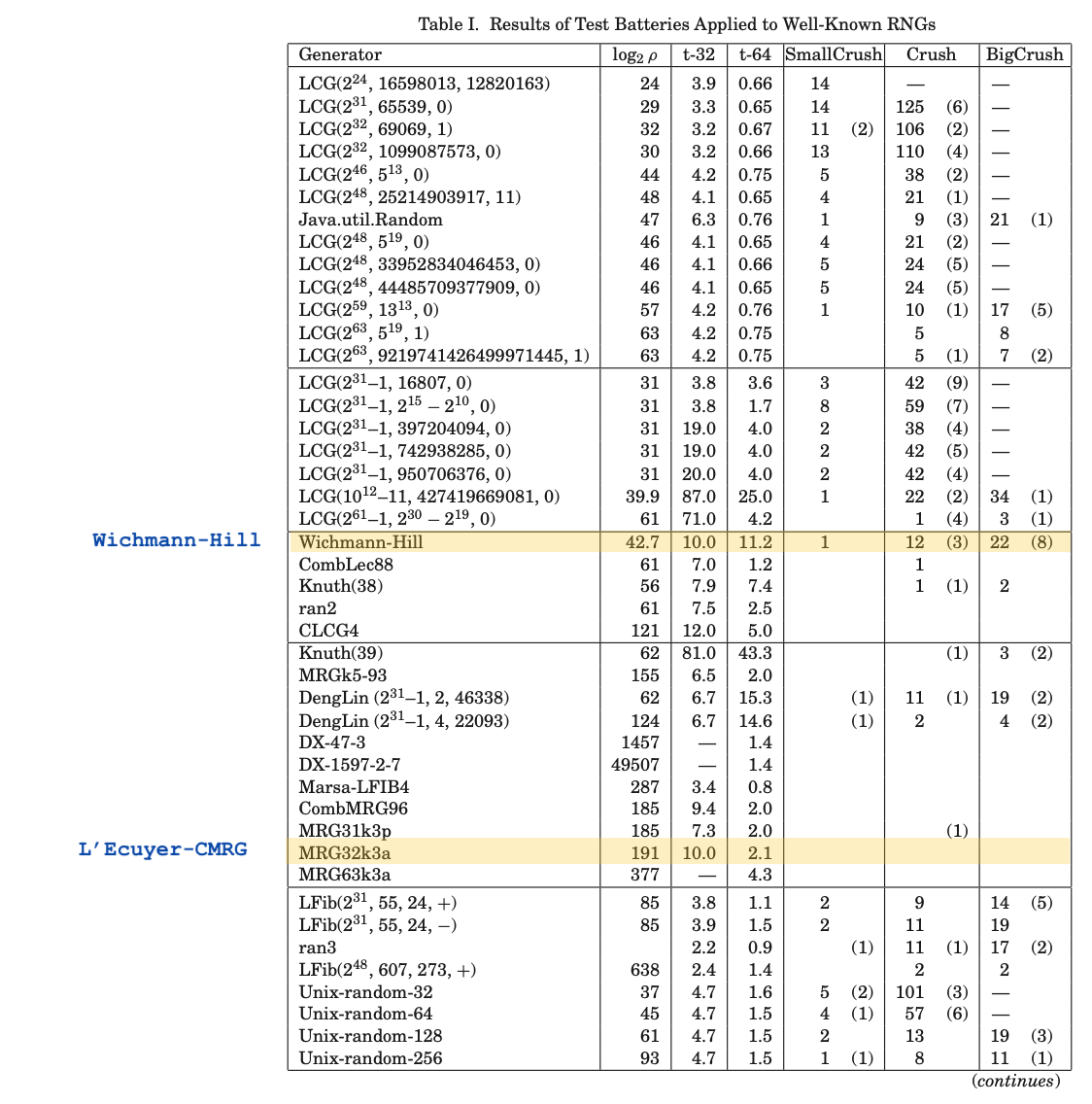
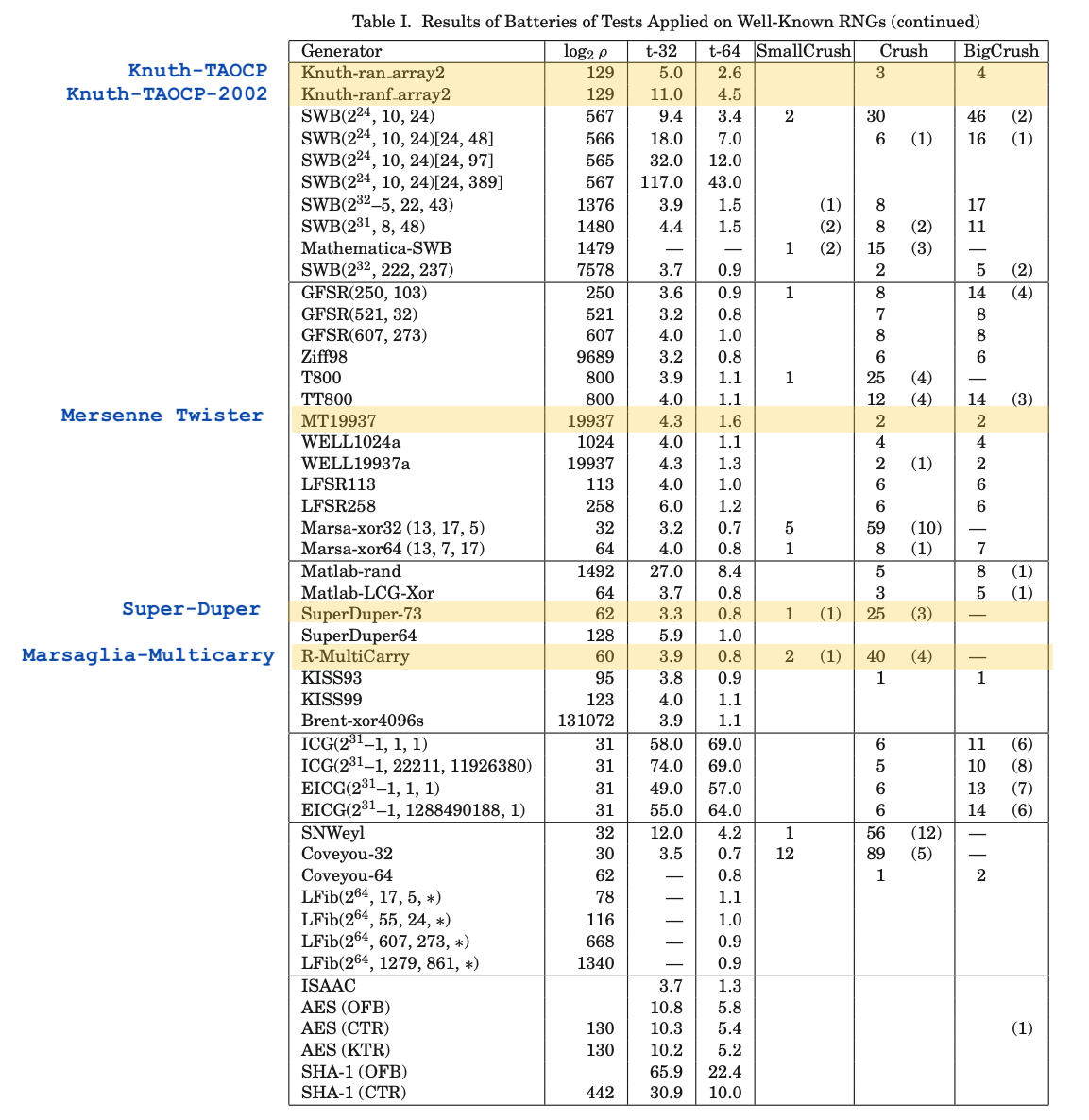
I’ve summarised Table 1 from this paper for the PRNGs which are available in base R. In this summary I only include the BigCrush numbers. The full version of Table 1 is included at the end of this post;
| Year | RNGkind | Alias | Big Crush Errors |
|---|---|---|---|
| 1970s | Super Duper | Super Duper 73 | Test not run as there were too many errors already at lower levels |
| 1982 | Wichmann-Hill | 22 | |
| 1997 | Mersenne Twister | MT19937 | 2 |
| 1997 | Marsaglia-Multicarry | R-Multicarry | Test not run as there were too many errors already at lower levels |
| 1997 | Knuth-TAOCP | Knuth.ran_array2 | 4 |
| 1999 | L’Ecuyer-CMRG | MRG32k3a | 0 |
| 2002 | Knuth-TAOCP-2002 | Knuth.ranf_array2 | 0 |
Notes on built-in PRNG quality:
- R’s default PRNG (Mersenne-Twister) fails 2 test on BigCrush
- Only L’Ecuyer and Knuth-TAOCP-2002 pass the BigCrush tests with no failures
- The other PRNGs seem to perform quite badly with either multiple failures on BigCrush, or so many failures on SmallCrush and Crush that it wasn’t even worth testing then on BigCrush
- There appears to be a trend that more recent PRNGs have fewer failures on BigCrush.
- The most recent PRNG is 18 years old! What’s happened since then in PRNG development?
Testing built-in PRNGs for speed
Click to show/hide benchmark code
library(ggplot2)
library(bench)
rng_kinds <- c(
'Mersenne-Twister',
'Wichmann-Hill',
'Marsaglia-Multicarry',
'Super-Duper',
'Knuth-TAOCP-2002',
'Knuth-TAOCP',
"L'Ecuyer-CMRG"
)
N <- 1e6
fun <- function(rng_kind) {
RNGkind(kind = rng_kind)
res <- bench::mark(runif(N))
res$expression <- rng_kind
res
}
baser <- lapply(rng_kinds, fun)
baser <- do.call(rbind, baser)
plot(baser) +
labs(title = "Benchmark: runif() generation of 1e6 random numbers")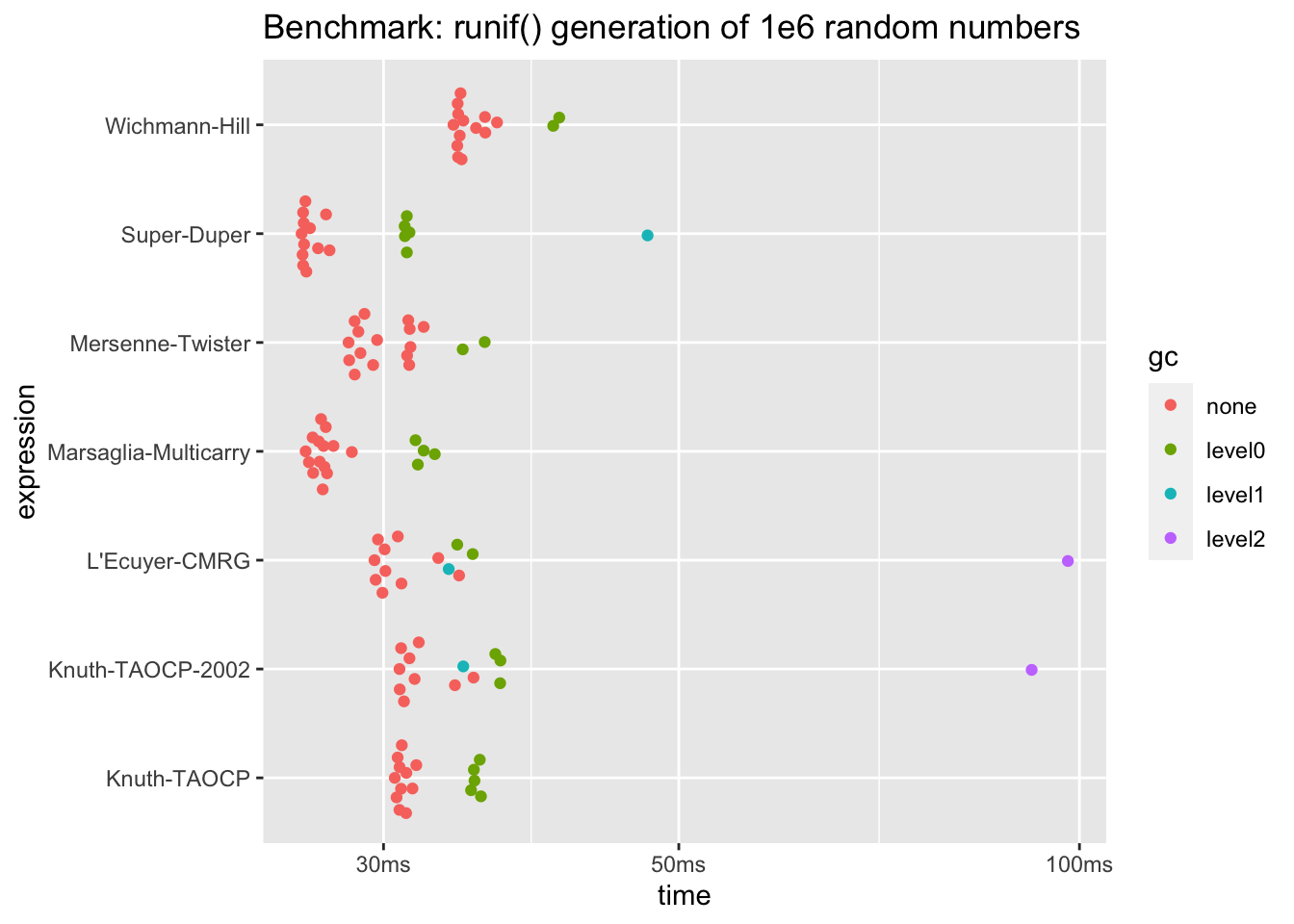
Notes on built-in PRNG speed:
- All the built-in PRNGs are about the same speed
- Not sure if this is a characteristic of the way they are included within R - there may be a lot of setup/call overhead that is overshadowing the timing of the actual random number generation.
Appendix: Full PRNG comparison table.
This is an extract from L’Ecuyer’s TestU01: A C Library for Empirical Testing of Random Number Generators (pdf)
How to read this table:
- The numbers in the last 3 rows are the number of failures for a particular
statistical test i.e. SmallCrush, Crush and BigCrush.
- A number in brackets e.g.
(12)indicates a suspect p-value, but not necessarily a failure.
- A number in brackets e.g.
- The second column is the log2 of the period of the generator (how long before it loops back to the start)
t-32andt-64are the times to generate 10^8 random numbers on a 32 and 64-bit machine (see the paper for actual specs)
Appendix: Other resources:
- Correction to random number generation in R3.6.0 - here and here
- John Cook looks at few modern PRNGs in his 2017 blog post Testing RNGs with PractRand
- PCG PRNG
- Some criticism on the claims around PCG - here
- Good Practice in (Pseudo) Random Number Generationfor Bioinformatics Applications