The Queen’s Gambit - Post 2
Inspired by The Queen’s Gambit on Netflix, I’m doing a few posts on Chess in R.
This screenshot from the show explains everything:

Introduction to the Knight’s Tour problem
The knight’s tour is a sequence of moves of a single knight such that it visits every square on the board once only.
The wikipedia page is a good starting resource.
This post contains:
- A recursive function for finding a solution given a starting move:
move_knight() - A solution to the knight’s tour that fits in a tweet
Recursive solution in R for the Knight’s Tour Problem
The following code finds an 8x8 knight’s tour in less than a second.
library(purrr)
library(dplyr)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Knight offsets i.e. the possible movements of a knight from the current location
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
knight_offsets <- matrix(c(
1, 2,
2, 1,
-2, 1,
-1, 2,
2, -1,
1, -2,
-1, -2,
-2, -1
), ncol = 2, byrow = TRUE)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#' Recurisvely calculate moves for a knight to complete a tour
#'
#' @param this_move proposed next move. 2 element numeric vector of (row, col)
#' position at which to place the knight next
#' @param moves list of vectors. Each vector is length=2 and indicates the
#' row/column locations of the knight's tour so far
#' @param visited 8x8 logical matrix which indicates whether or not a square has been
#' visited by the knight already. When called by the user, this matrix
#' must only contain FALSE
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
move_knight <- function(this_move, moves, visited) {
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Mark the move as visited
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
moves <- append(moves, list(this_move))
visited[this_move[1] + (this_move[2] - 1)*8] <- TRUE
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# termination if all visited
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
if (all(visited)) {
return(moves)
}
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Find all possible moves from this position
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
next_move <- cbind(knight_offsets[,1] + this_move[1], knight_offsets[,2] + this_move[2])
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# keep only moves that remain on the board
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
on_board <- next_move[,1] %in% 1:8 & next_move[,2] %in% 1:8
next_move <- next_move[on_board,,drop=FALSE]
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Keep only moves that target a location that has not yet been visited
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
not_yet_visited <- !visited[next_move]
next_move <- next_move[not_yet_visited,, drop = FALSE]
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Recurse over every possible next move
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
for (i in seq_len(nrow(next_move))) {
res <- move_knight(next_move[i,, drop = FALSE], moves, visited)
if (!is.null(res)) {
return(res)
}
}
NULL
}Find a knight’s tour and plot it
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Find a tour from the given starting position
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
system.time({
moves <- move_knight(c(4, 8), moves = list(), visited = matrix(FALSE, 8, 8))
})## user system elapsed
## 0.192 0.012 0.204#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#' Convert results to a data.frame for ggplot
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
moves_df <- as.data.frame(do.call(rbind, moves))
moves_df <- set_names(moves_df, c('x', 'y'))
moves_df$idx <- 1:nrow(moves_df)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
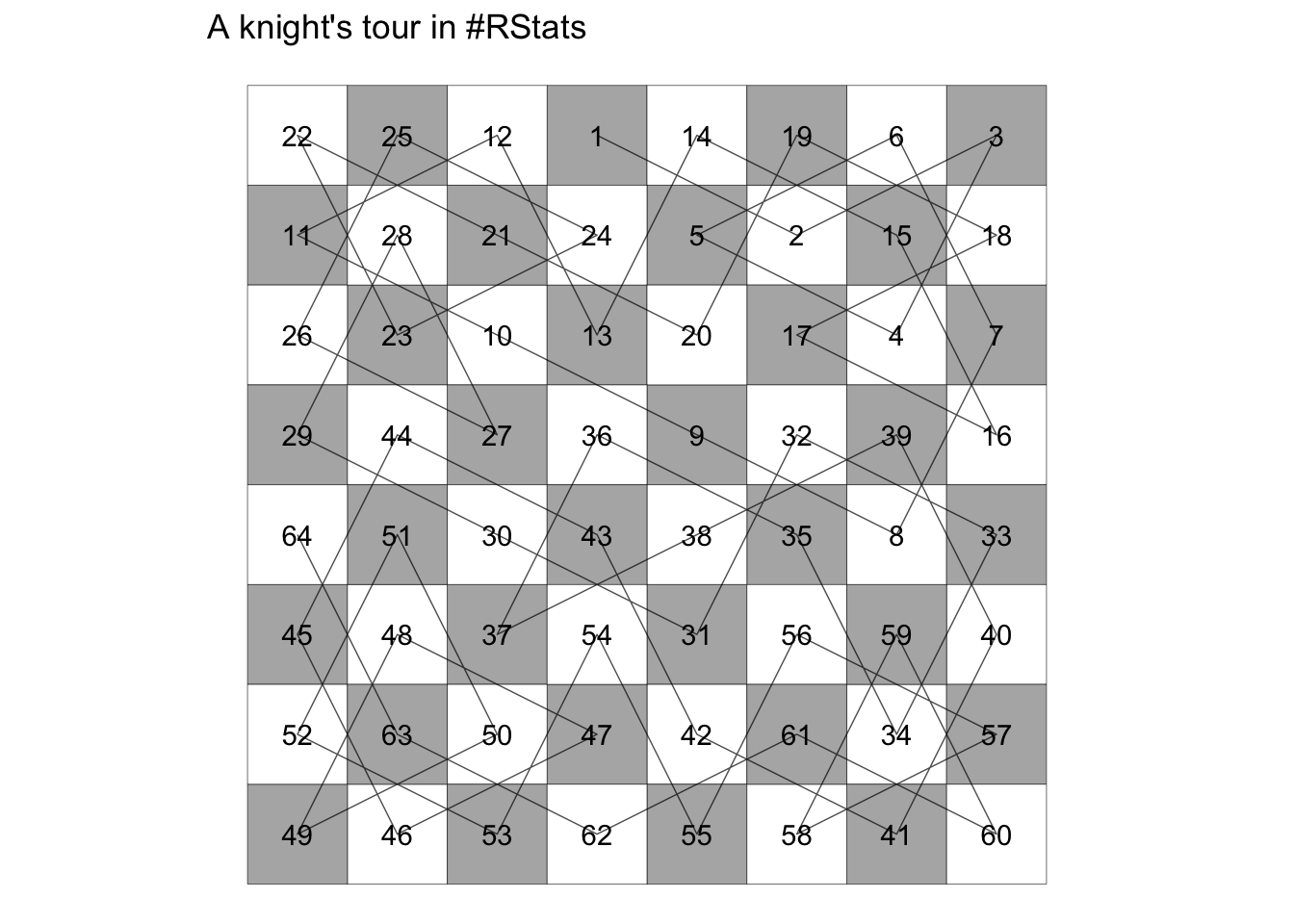
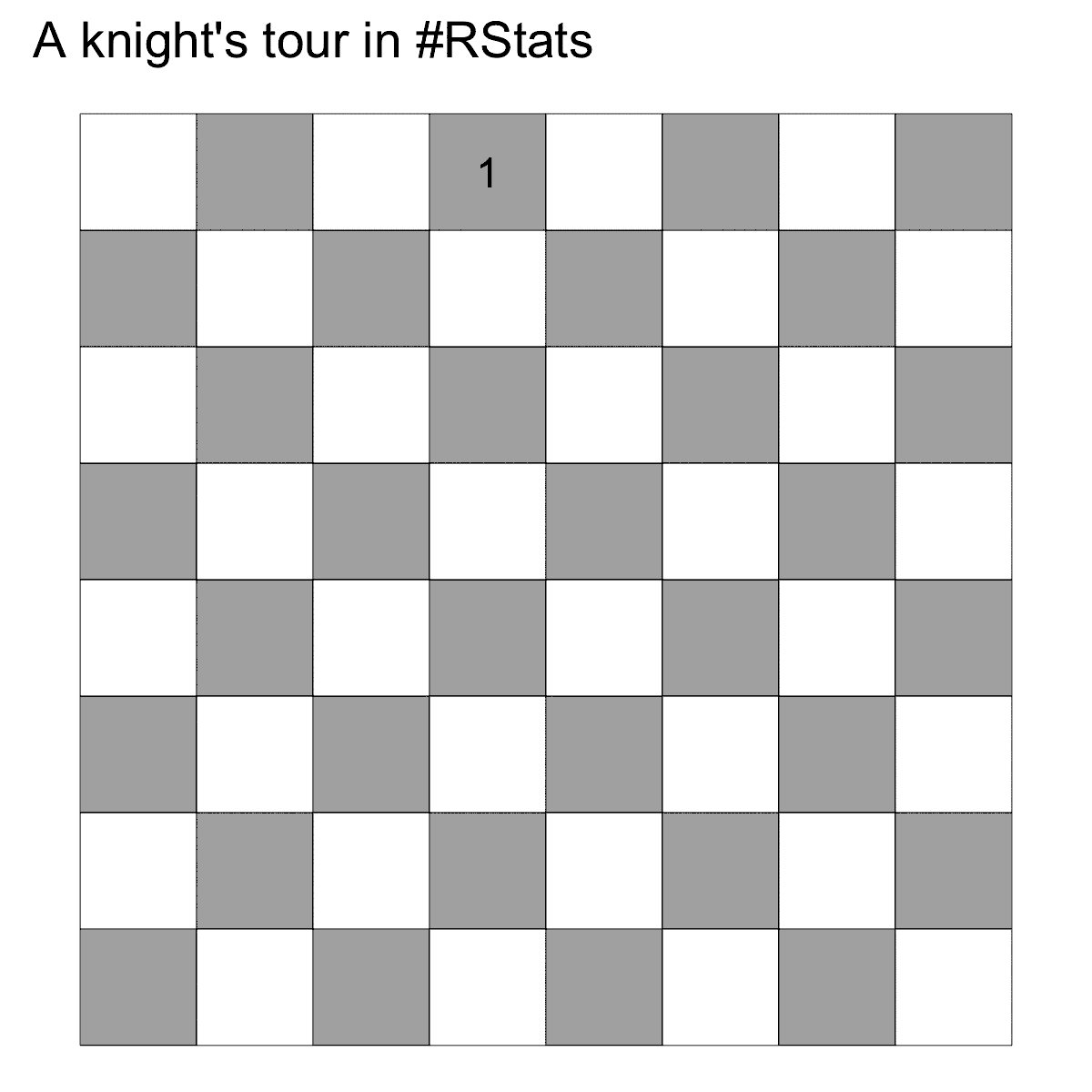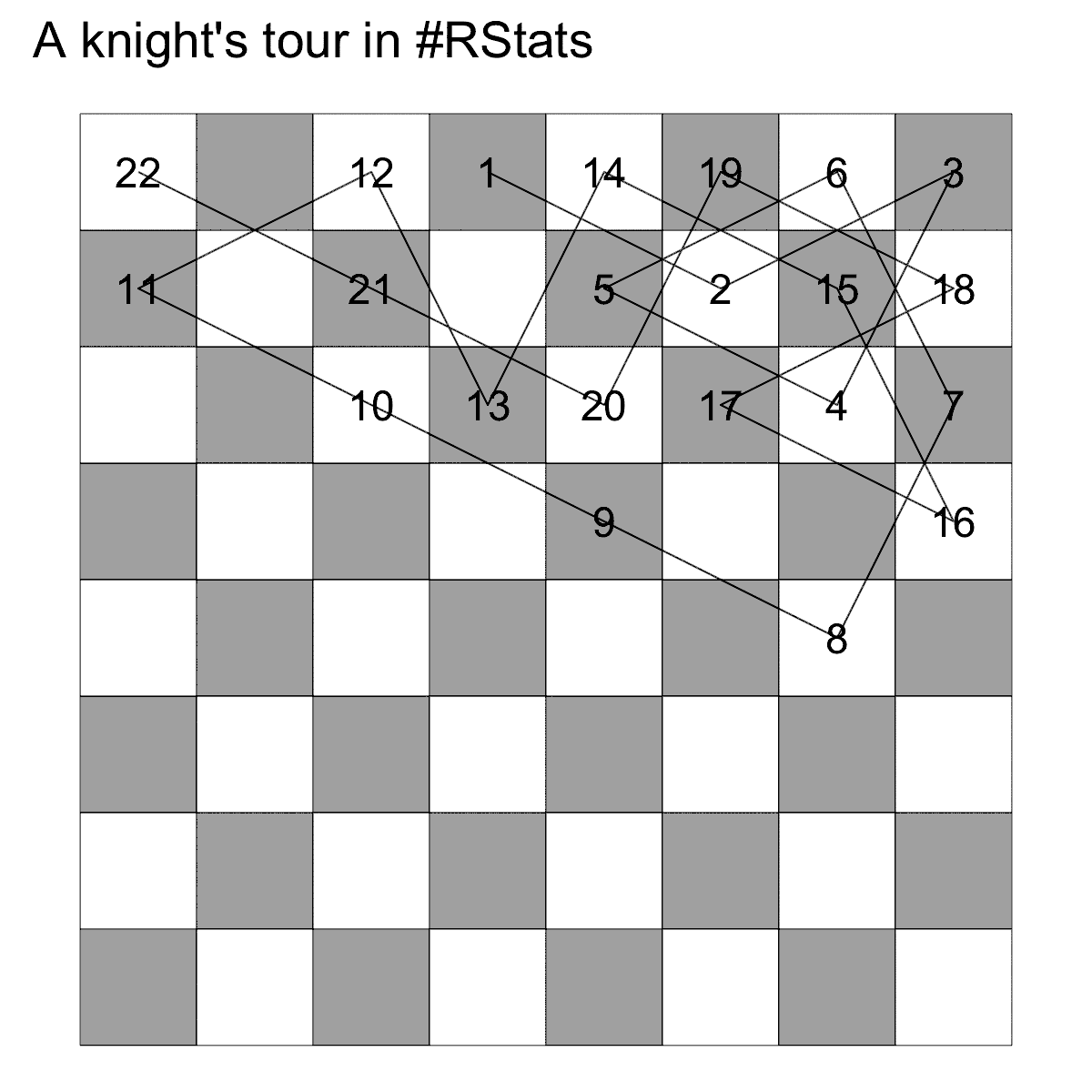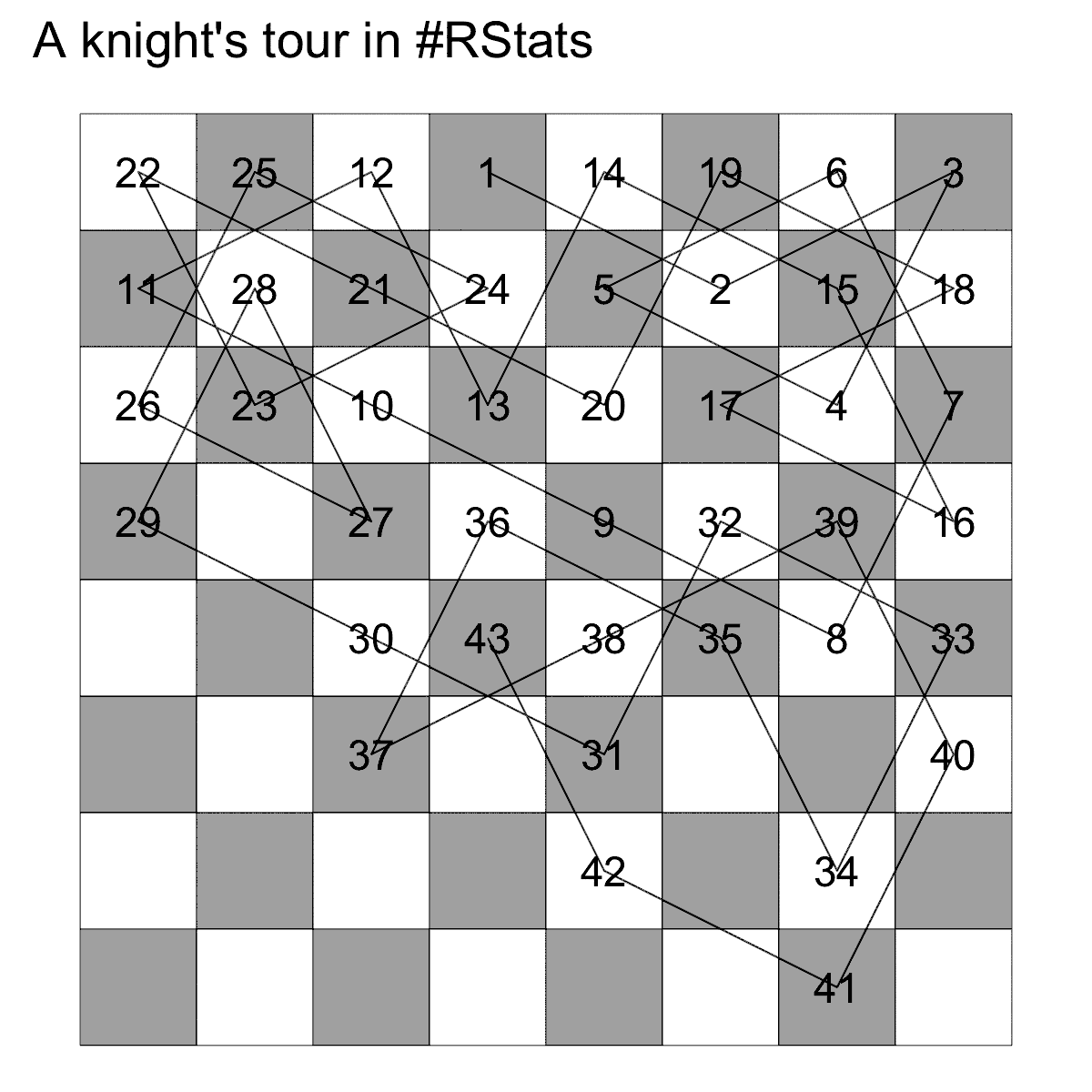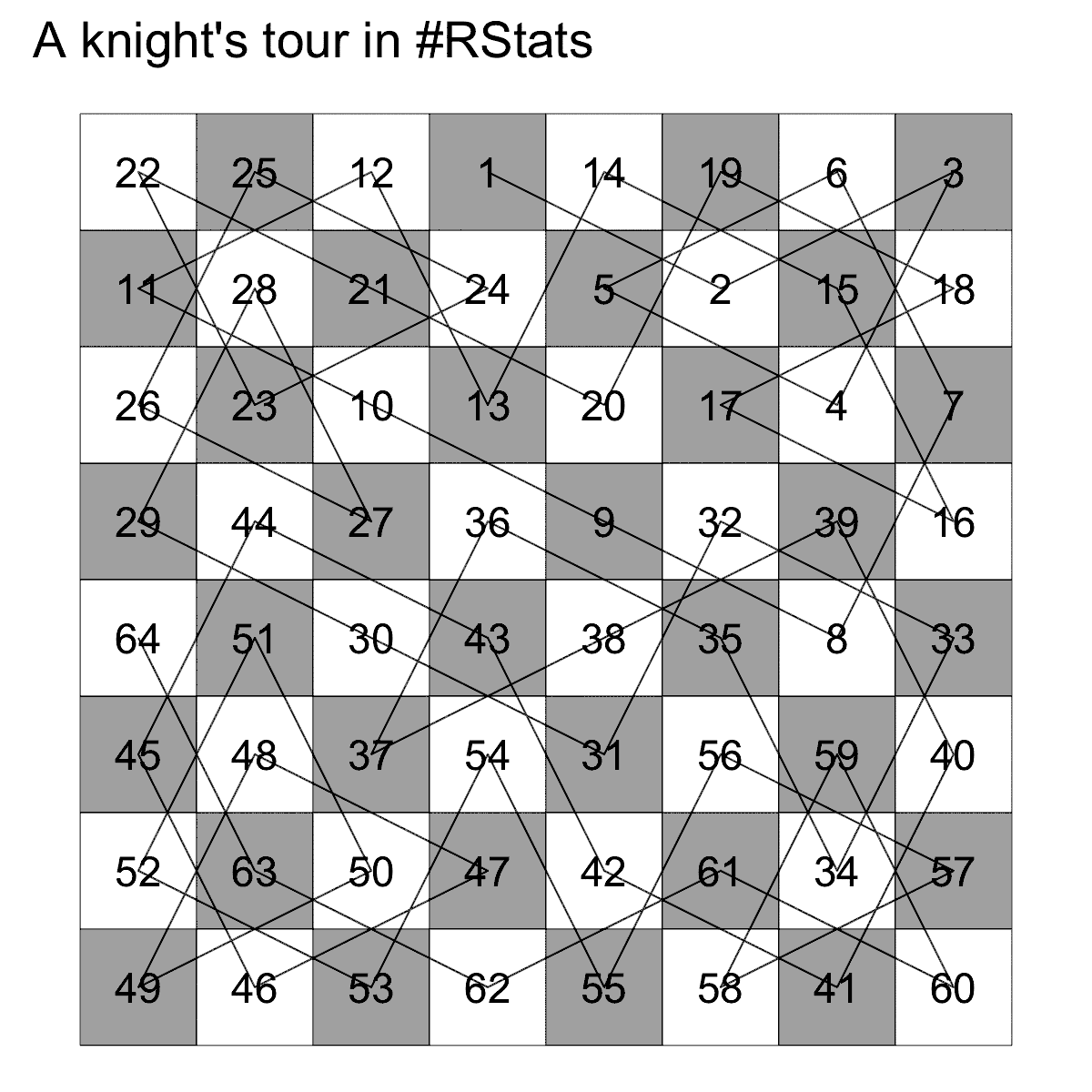
# Plot the knight's tour
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ggplot(moves_df, aes(x, y)) +
geom_tile(aes(fill=as.logical((x+y)%%2)), colour = 'black') +
geom_path(alpha = 0.7, linetype = 1, size = 0.25) +
geom_text(aes(label = idx)) +
scale_fill_manual(values = c('grey70', 'white')) +
theme_void() +
theme(legend.position = 'none') +
coord_equal() +
labs(
title = "A knight's tour in #RStats"
)
An animation of the Knight’s Tour
Tweet-length Knight’s Tour
The following tweet-able code generates a knight’s tour on an 8x8 chess board.
The list of values returned is a list of
#RStats
s=1:2;t=2:1;A=matrix;R=return
f=function(m,M,v){M=rbind(M,m)
v[m]=T
if(all(v))R(M)
N=cbind(c(s,-t,t,-s)+m[1],c(t,s,-s,-t)+m[2])
N=N[N[,1]%in%1:8&N[,2]%in%1:8,,drop=F]
N=N[!v[N],,drop=F]
for(i in row(N)[,1])if(length((r=f(N[i,,drop=F],M,v))))R(r)}
f(A(s*4,1),c(),A(F,8,8))Running this code produces a set of 64 locations which are a knight’s tour of an 8x8 chess board.
Click to reveal/hide the solution matrix of knight locations
[,1] [,2]
[1,] 4 8
[2,] 6 7
[3,] 8 8
[4,] 7 6
[5,] 5 7
[6,] 7 8
[7,] 8 6
[8,] 7 4
[9,] 5 5
[10,] 3 6
[11,] 1 7
[12,] 3 8
[13,] 4 6
[14,] 5 8
[15,] 7 7
[16,] 8 5
[17,] 6 6
[18,] 8 7
[19,] 6 8
[20,] 5 6
[21,] 3 7
[22,] 1 8
[23,] 2 6
[24,] 4 7
[25,] 2 8
[26,] 1 6
[27,] 3 5
[28,] 2 7
[29,] 1 5
[30,] 3 4
[31,] 5 3
[32,] 6 5
[33,] 8 4
[34,] 7 2
[35,] 6 4
[36,] 4 5
[37,] 3 3
[38,] 5 4
[39,] 7 5
[40,] 8 3
[41,] 7 1
[42,] 5 2
[43,] 4 4
[44,] 2 5
[45,] 1 3
[46,] 2 1
[47,] 4 2
[48,] 2 3
[49,] 1 1
[50,] 3 2
[51,] 2 4
[52,] 1 2
[53,] 3 1
[54,] 4 3
[55,] 5 1
[56,] 6 3
[57,] 8 2
[58,] 6 1
[59,] 7 3
[60,] 8 1
[61,] 6 2
[62,] 4 1
[63,] 2 2
[64,] 1 4