isocubes

{isocubes} is an isometric rendering canvas with cubes as the only graphics primitive.

What’s in the box

isocubesGrob() to convert 3d integer coordinates into a grob for plotting
coord_heightmap() to create coordinates for a heightmap from a matrix and (optional) colour information
coord_sphere() to create coordinates for all isocubes within a sphere

Coordinate system

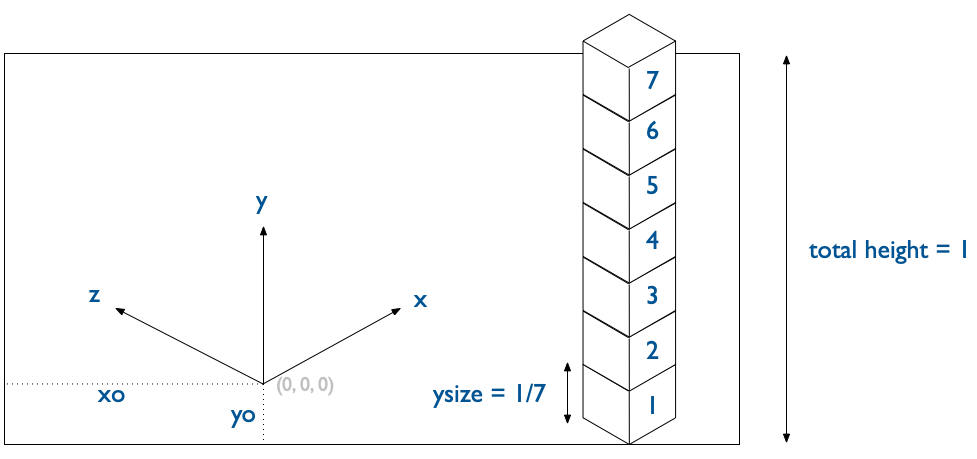
The size and positioning of the isometric coordinate system is controlled by arguments isocubesGrob(coords, max_y, xo, yo)
xo and yo give the positition of the origin of the isometric view within the graphics window. These are fractional values which will be interpreted as snpc units i.e. fractional width and height of the graphics devices.
max_y is the main control for cube sizing. This value is the number of cubes that can be stacked to fill the vertical extents of the window. Higher values of max_y means smaller cubes.
The isometric view is a left-handed coordinate system with y vertical.
The (x, y, z) coordinates given to position the cubes will be rounded to the nearest integer. There is no fractional positioning of cubes.

Why isometric?

Isometric cubes have advantages over other axonometric and perspective coordinate systems:

No perspective correction needed.
No foreshortening along different dimensions.
The cube is just a hexagon with each third shaded differently, and the polygons for each face are trivial to calculate and draw.
The rules for occlusion are simple i.e. it’s easy to cull cubes from the drawing process if they’re hidden behind other cubes and won’t be seen. Fewer cubes mean a faster rendering time.

Installation

You can install from GitHub with:

# install.package('remotes')
remotes::install_github('coolbutuseless/isocubes')

‘R’ in isocubes

library(grid)
library(purrr)
library(isocubes)

x <- c(9, 8, 7, 6, 5, 4, 3, 2, 10, 9, 3, 2, 11, 10, 3, 2, 11, 10, 
3, 2, 11, 10, 3, 2, 11, 10, 3, 2, 10, 9, 3, 2, 9, 8, 7, 6, 5, 
4, 3, 2, 10, 9, 3, 2, 11, 10, 3, 2, 11, 10, 3, 2, 11, 10, 3, 
2, 11, 10, 3, 2, 11, 10, 3, 2, 11, 10, 3, 2)

y <- c(15, 15, 15, 15, 15, 15, 15, 15, 14, 14, 14, 14, 13, 13, 13, 
13, 12, 12, 12, 12, 11, 11, 11, 11, 10, 10, 10, 10, 9, 9, 9, 
9, 8, 8, 8, 8, 8, 8, 8, 8, 7, 7, 7, 7, 6, 6, 6, 6, 5, 5, 5, 5, 
4, 4, 4, 4, 3, 3, 3, 3, 2, 2, 2, 2, 1, 1, 1, 1)

coords <- data.frame(x = x, y = y, z = 0)
cubes  <- isocubesGrob(coords, max_y = 25)
grid.newpage(); grid.draw(cubes)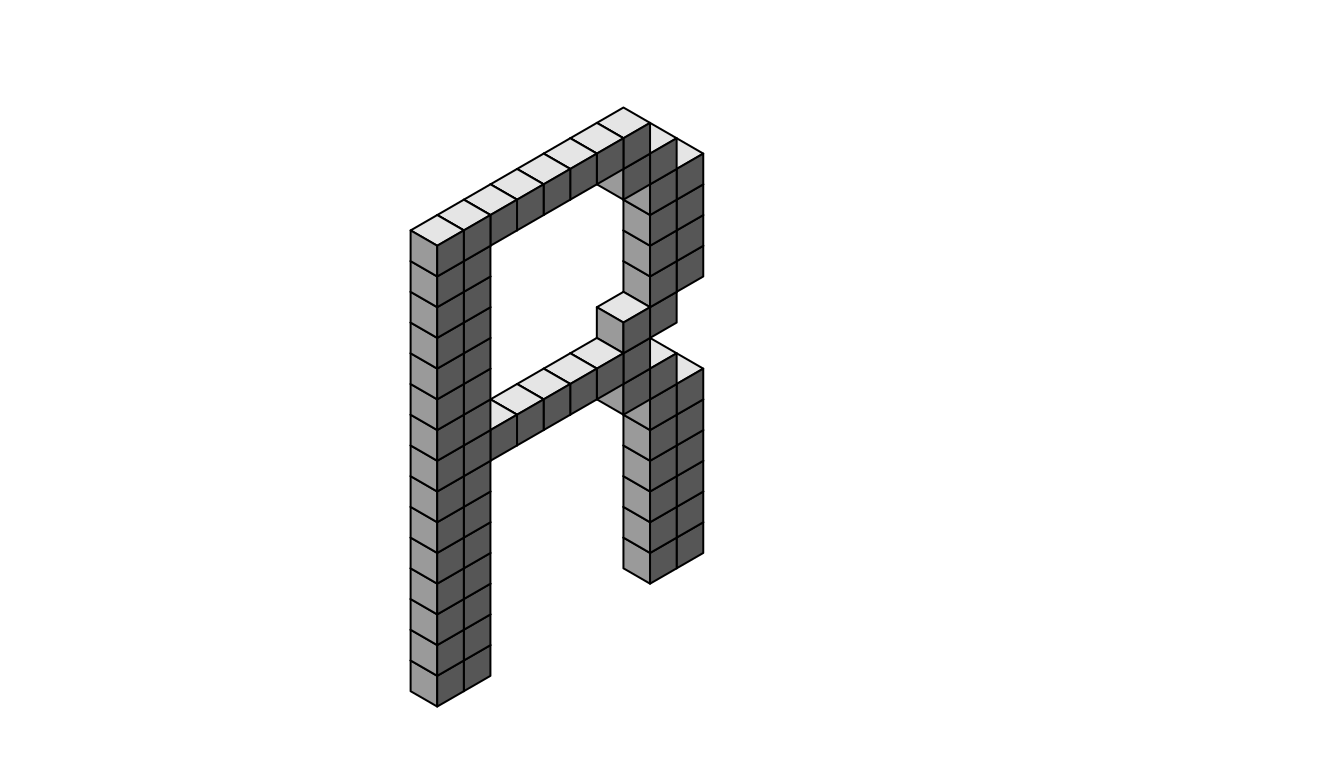

# Colour the cubes with rainbow
cubes <- isocubesGrob(coords, fill = rainbow(nrow(coords)), max_y = 25)
grid.newpage(); grid.draw(cubes)

# VaporWave palette
cubes <- isocubesGrob(coords, fill = '#ff71ce', fill_left = '#01cdfe',
                      fill_right = '#05ffa1', max_y = 25)
grid.newpage(); grid.draw(cubes)

# Nightmare palette
cubes <- isocubesGrob(coords, 
                      fill = rainbow(nrow(coords)), 
                      fill_left = 'hotpink',
                      fill_right = viridisLite::inferno(nrow(coords)), 
                      max_y = 25, col = NA)
grid.newpage(); grid.draw(cubes)

Calculate isocubes within a sphere

library(grid)
library(isocubes)

N      <- 13
coords <- expand.grid(x=seq(-N, N), y = seq(-N, N), z = seq(-N, N))
keep   <- with(coords, sqrt(x * x + y * y + z * z)) < N
coords <- coords[keep,]

cubes <- isocubesGrob(coords, max_y = 35, xo = 0.5, yo = 0.5)
grid.newpage()
grid.draw(cubes)

Random rainbow volume of isocubes

library(isocubes)

N      <- 15
coords <- expand.grid(x=0:N, y=0:N, z=0:N)
coords <- coords[sample(nrow(coords), 0.66 * nrow(coords)),]
fill   <- rgb(red = 1 - coords$x / N, coords$y /N, 1 - coords$z/N, maxColorValue = 1)

cubes <- isocubesGrob(coords, fill, max_y = 40, occlusion_depth = 4)
grid.newpage()
grid.draw(cubes)

Heightmap as isocubes

#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Prepare a matrix of values
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
mat <- volcano

#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# An optional matrix of colours
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
val <- as.vector(mat)
val <- round(255 * (val - min(val)) / diff(range(val)))
col <- viridisLite::viridis(256)[val + 1L]
dim(col) <- dim(mat) 

#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Find the (integer) coordiinates of the cubes in the heightmap
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
coords <- coords_heightmap(mat - min(mat), col = col, scale = 0.3)

#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Convert the coordinates into a grob
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
cubes  <- isocubesGrob(coords, max_y = 100, fill = coords$col, xo = 0.8)
grid.newpage(); grid.draw(cubes)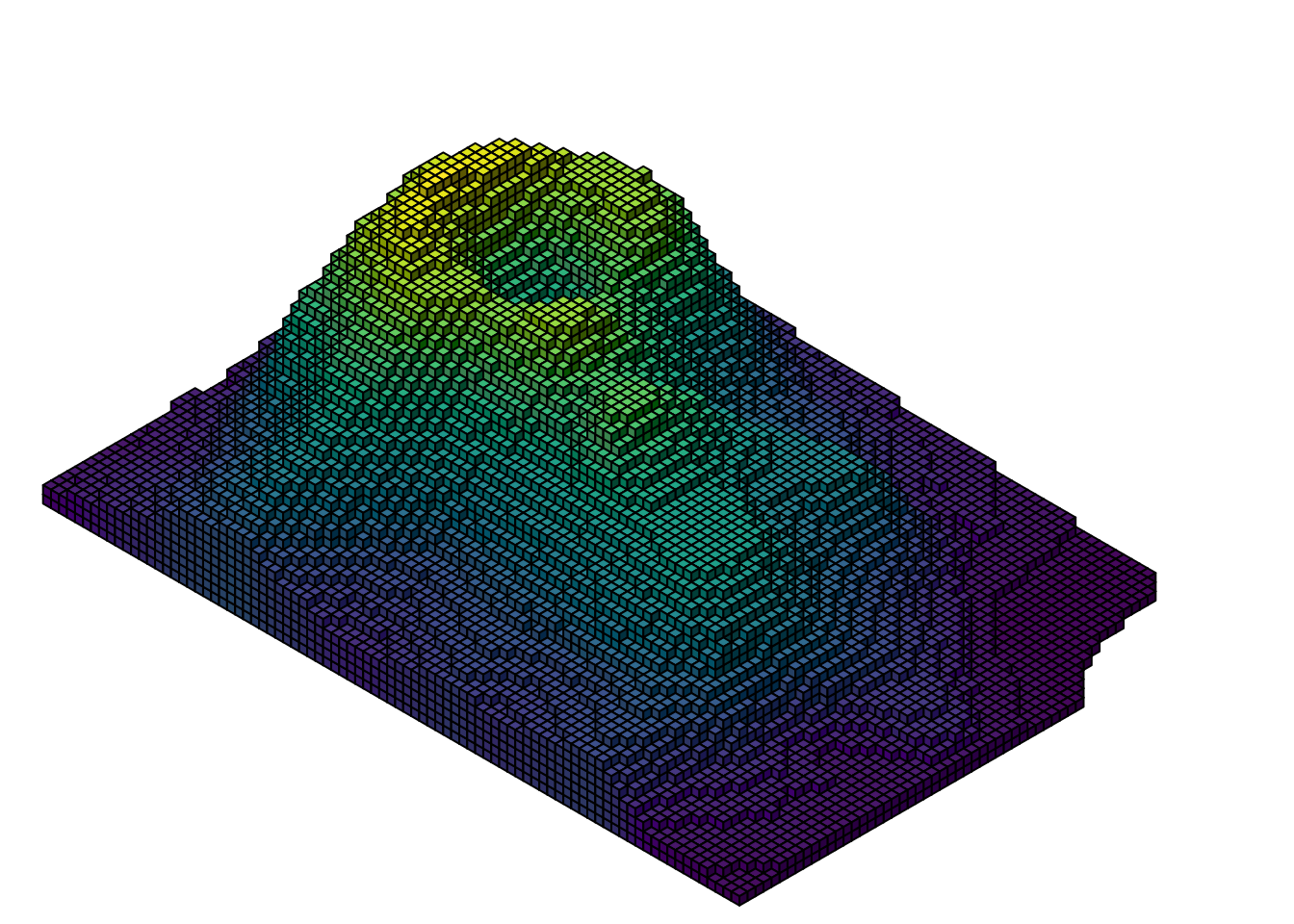

Image as isocubes

Treat image to a heightmap

#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Load image and convert to a matrix of heights
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
img <- png::readPNG("../../static/img/isocubes/Rlogo-small-blur.png")
ht        <- round( 10 * (1 - img[,,2]) ) # Use Green channel intensity as height
ht[,1]    <- 0 # image editing to remove some artefacts

#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# A matrix of colours extracted from the image
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
col       <- rgb(img[,,1], img[,,2], img[,,3])
dim(col)  <- dim(ht) 

#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# convert to cubes and draw
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
coords <- coords_heightmap(ht, col = col, ground = 'xy')
cubes  <- isocubesGrob(coords, max_y = 130, fill = coords$col, col = NA)
grid.newpage(); grid.draw(cubes)

Technical Bits

Cube occlusion

In an isometric view, a cube at position (x, y, z) will block the view of any cube at (x + n, y - n, z + n).

Since cube positions must be integer values, hashes of cube positions are calculated as x + (y * 256) + (z * 256^2).

For each initial cube position, calculate the hash or coordinates of several occluded cubes. Then remove any initial cubes which match the occluded cube hashes.

Cube sort

Arrange cubes by -x, -z then y to ensure cubes are drawn in the correct ordering such that cubes in front are drawn over the top of cubes which are behind.

grob

All the faces of all the cubes are then calculated as polygons - each with 4 vertices.

The data for all polygons is then concatenated into a single polygonGrob() call with an appropiate vector for id.lengths to split the data.

Acknowledgements

R Core for developing and maintaining the language.
CRAN maintainers, for patiently shepherding packages onto CRAN and maintaining the repository

Introducing isocubes - an isometric rendering backend