Nonograms
Nonograms are picture logic puzzles in which cells in a grid must be colored or left blank according to numbers at the side of the grid to reveal a hidden picture.
That is, the numbers on the side of the image (the clues) are the run-length encoding of the filled-in squares for each row and column.
By simultaneously satisfying the clues for the rows and columns, a picture is revealed!
In this short series of posts I will:
- Introduce the nonogram package (previous post).
- Show how to make nonograms by hand, or from an existing image (previous post.
- Describe the solution techniqe behind the package (this post).
The nonogram package
The nonogram package contains tools for plotting, solving and creating nonogram puzzles.
You can install nonogram from github with:
# install.packages("devtools")
devtools::install_github("coolbutuseless/nonogram")Nomenclature
clue
A clue is sequence of integers which are the run-length encoding of the filled-in squares in a row or column.
E.g. 1,2 is a clue which means that there is 1 filled-in square in this row
(or column) followed by some blank squares, and then two filled-in squares in a row
pattern
A pattern is a sequence of filled-in and blank squares which make up a row or column.
E.g. the clue 1,2 (on a board 8 squares wide) is satisfied by each
of the following patterns, represented as a matrix and shown graphically
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 0 1 0 1 1 0 0 0
[2,] 0 0 1 0 0 1 1 0
[3,] 0 1 0 0 0 0 1 1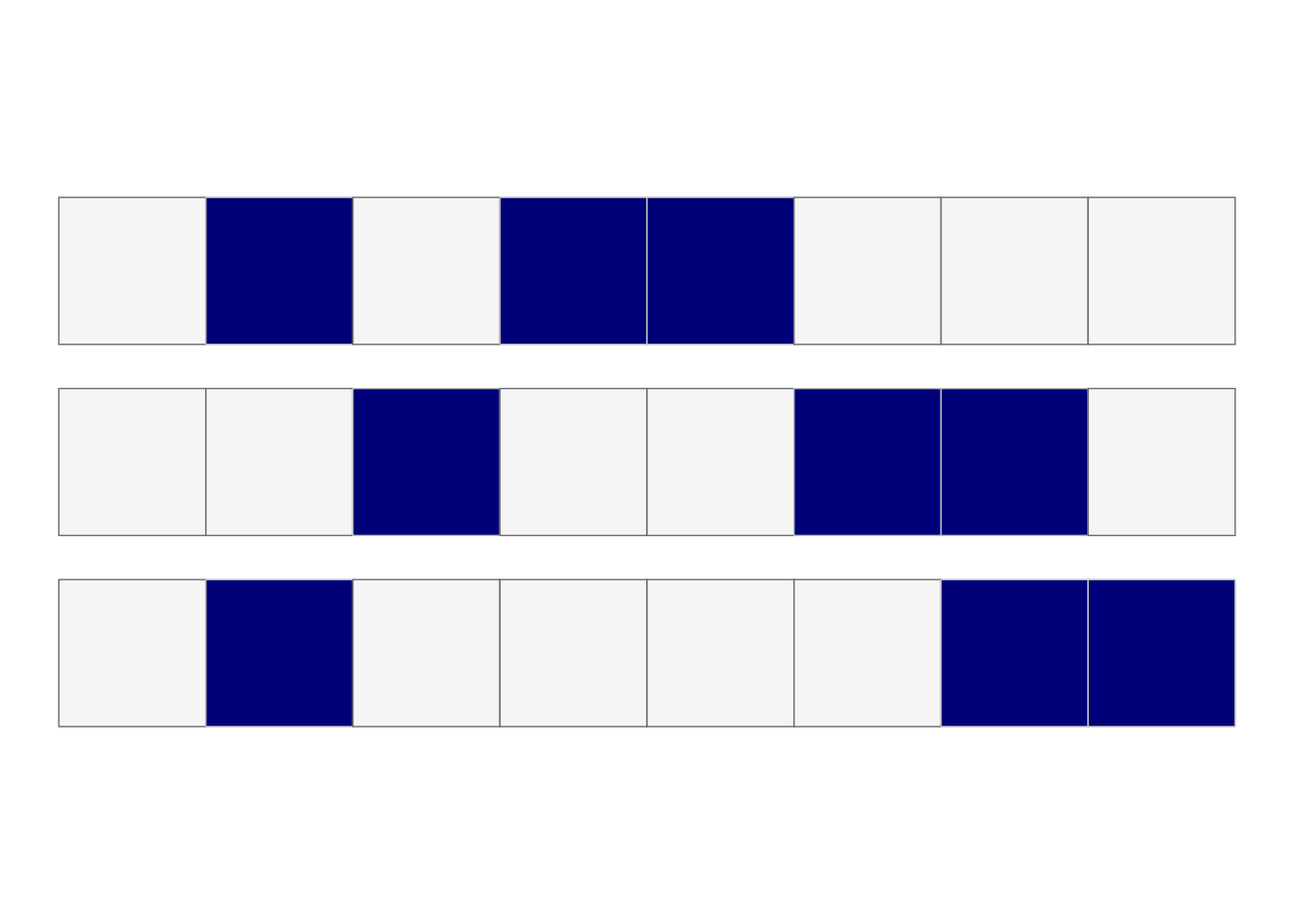
pattern set
A pattern set is the complete set of all possible patterns which satisfy a clue.
E.g. the pattern set for the clue 2,3 on a board 8 squares wide is shown below
as a matrix as well as graphically.
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 0 1 1 0 1 1 1 0
[2,] 1 1 0 1 1 1 0 0
[3,] 1 1 0 0 1 1 1 0
[4,] 0 1 1 0 0 1 1 1
[5,] 0 0 1 1 0 1 1 1
[6,] 1 1 0 0 0 1 1 1
pattern sets
For each clue along the rows, and each clue along the columns, there is a pattern set.
The row pattern sets is the collection of the pattern sets for every row.
The column pattern sets is the collection of the pattern sets for every column.
puzzle
A puzzle is collection of clues, represented in the nonogram package as a list of
vectors.
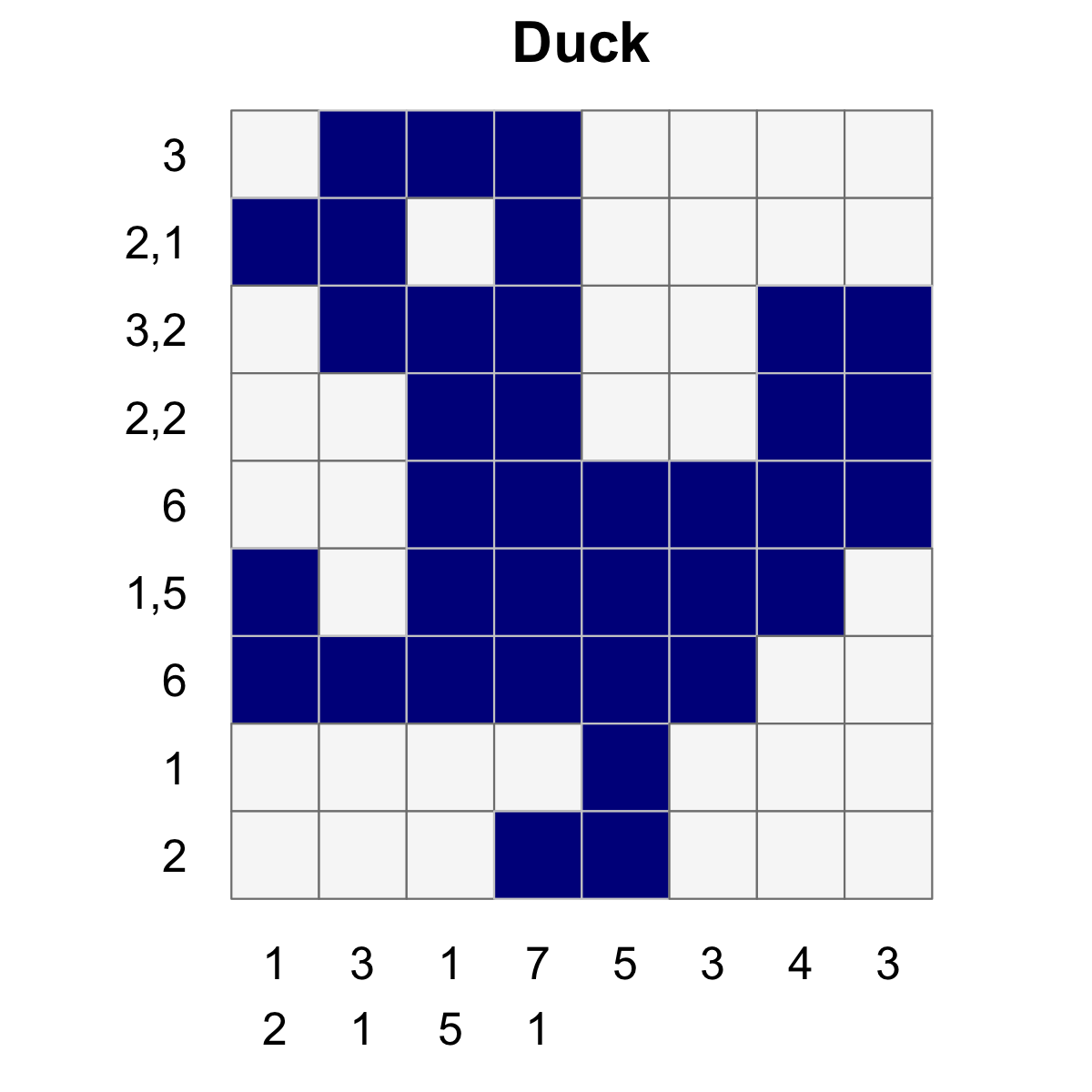
E.g. the puzzle for the duck image shown at the top is:
puzzle <- list(
row_clues = list(3L, 2:1, 3:2, c(2L, 2L), 6L, c(1L, 5L), 6L, 1L, 2L),
col_clues = list(1:2, c(3L, 1L), c(1L, 5L), c(7L, 1L), 5L, 3L, 4L, 3L)
)puzzle string
For storage and transfer, it’s sometimes easier to deal with the puzzle just as a string.
A puzzle string is a compact string representation of the puzzle.
It consists of:
- the numbers for each clue separated by a comma
- each clue separated by a colon
- the row and column clues (in that order) separated by a dash
As an example, the following is the puzzle string for the duck nonogram
"3:2,1:3,2:2,2:6:1,5:6:1:2-1,2:3,1:1,5:7,1:5:3:4:3"Solution technique
- For each clue generate its pattern set
- Within each pattern set, find if any locations are a constant colour, and use this fact to elimintate patterns in the other direction
- On the remaining (hopefully small) number of choices within each pattern set for each clue, do a recursive search with back-tracking to find a solution
Solution step 1: Generate all possible patterns for a clue
This was the most difficult part of this solution technique, as the number of
possible combinations, and the resulting pattern set, can be huge.
Most grids in print max out at about 35 squares along each side. There are plenty of larger ones, but I optimised the solver only up to this size.
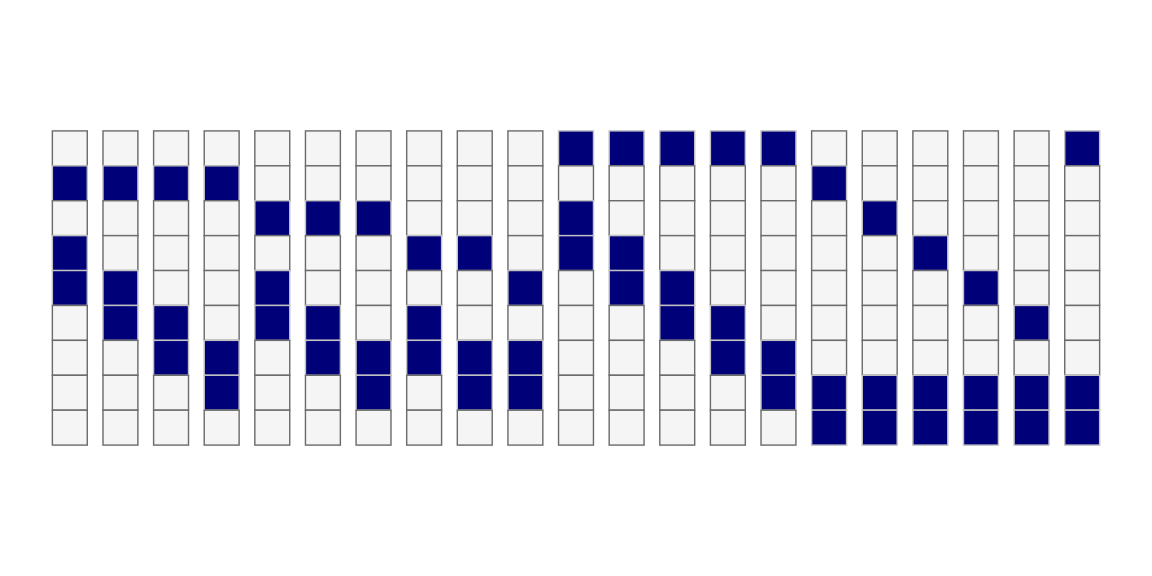
For a small puzzle, like the duck a the clue in the first column (1,2) has
21 possible patterns I’ve plotted them below
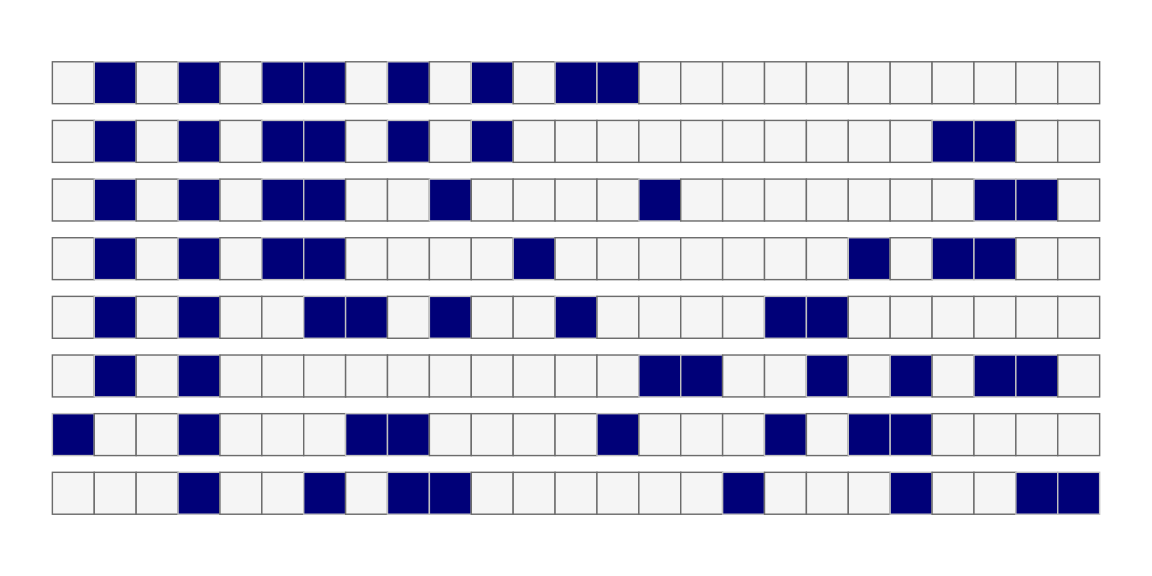
For the larger gchq puzzle below, the clue 1,1,2,1,1,2 to fit in the
puzzle width of 25 squares has 18,564 patterns, some of which are shown below.
For a clue of 1,1,2,1,1,2,1,1,1,1 in a puzzle that is 35 squares wide, there
are 1,961,256 patterns.
In the end, I’ve settled upon the following solution:
- recursively build the solution
- with back-tracking whenever a valid pattern is impossible from a particular location
- store all values as lists of matrices which allowed for fast filtering out of impossible pattern combinations
- have a cache of patterns for smaller clues and puzzle widths rather than recalcualting every time.
If I ever revisit this problem, I have an idea for a solution using the memoise package. But the problem with cacheing everything is that some of the pattern sets are HUGE - more than a gigabyte - and I don’t want to cache all those.
If I ever wanted to solve bigger nonograms, I’d need to use another solution technique altogether - the up-front generation of all possible clues just takes up too much time and memory.
Solution step 2: Filter the pattern sets
For very very small nonograms, it might be possible to try every combination of patterns in a row and exhaustively search for a solution.
In the duck problem the total number of combinations for all patterns for all rows is 8x10^6 (8 million). If you could try 10,000 patterns/sec, you could try them all in about 15 minutes.
For some of the larger nonograms there are more than 1x10^100 (not a typo) combinations to try if you wanted to brute force a solution!
To initally filter the set of all patterns into a more tractable solution, I look for locations within each pattern set which can only be one colour and use that to filter the orthogonal data set.
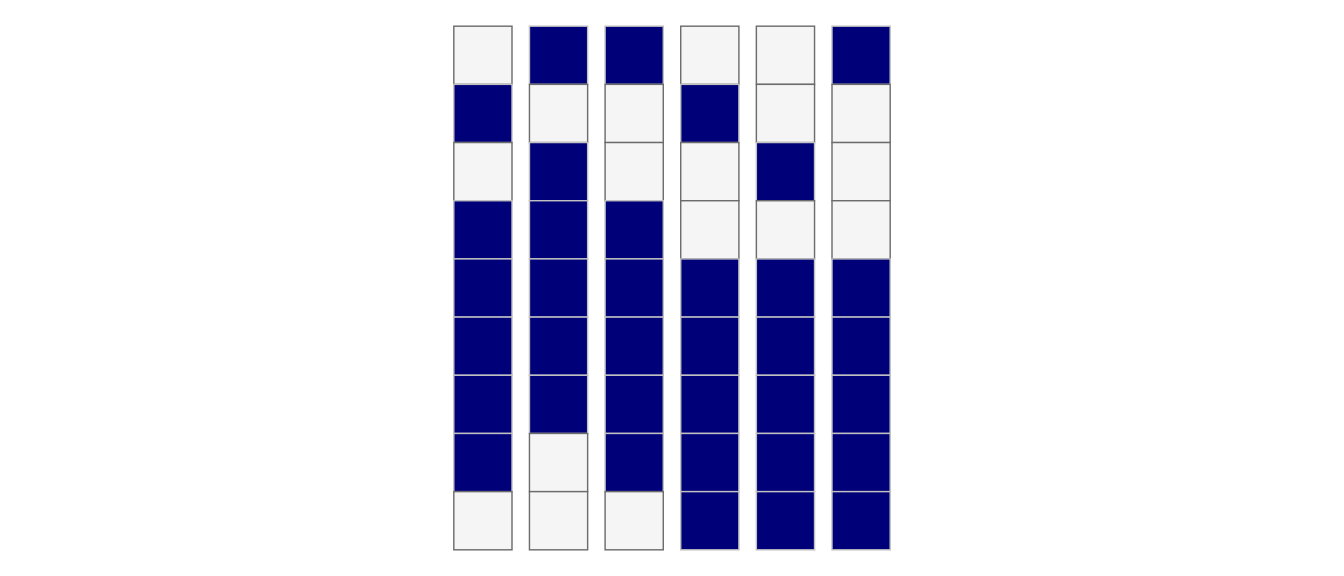
E.g. The pattern set for the third row in the duck puzzle with clue 3,2 is shown below:

The third column is always filled-in! Which means that I now look at the pattern sets for the third column and keep only ones with that location filled in.
The clue for the third column is 1,5 which looks like:
Only two patterns have the required filled-in square in the 3rd row, the others can be eliminated from consideration.
This process is repeated until there are no more occurrences.
Sometimes by doing this filtering there is only one possible pattern left for each row and column, in which case we have found a solution!
Solution step 3: Recursively build the solution by rows with back-tracking
If there are still multiple patterns to try for each row we now try all of them in turn by choosing them one row at a time.
But as each row is selected, a cross-check is done to see that at least one pattern in each column can fit that sequence of rows.
If it fails then we stop that search path, select a different row from the pattern set and continue.